Materiálové modely proudění
Vztah mezi rychlostí proudící kapaliny a změnou hydraulické výšky (pórového tlaku) je řízen Darcyho zákonem. Současná verze programu předpokládá konstantní hodnoty koeficientů filtrace. Závislost mezi součiniteli permeability a pórovým tlakem se neuvažuje.
Dále se zadává počáteční číslo pórovitosti zeminy e0 umožňující stanovit aktuální pórovitost zeminy n a následně skutečnou rychlost kapaliny proudící pouze póry vs=v/n, kde v je průměrná rychlost proudění celou průsakovou plochou. Obecně platí, že číslu pórovitosti e0 = 1 odpovídá pórovitost zeminy n = 50%.
Zavedením součinitele relativní permeability Kr umožňuje program sledovat přechod mezi plně nasyceným (S = 1,Kr = 1) a nenasyceným (Kr => 0) prostředím. Příkladem je řešení problému ustáleného proudění s volnou hladinou. Přechod mezi plně nasyceným a nenasyceným prostředím lze řídit jedním ze tří modelů vývoje součinitele relativní permeability Kr v závislosti na hodnotě pórového tlaku/tlakové výšky, viz obrázky.
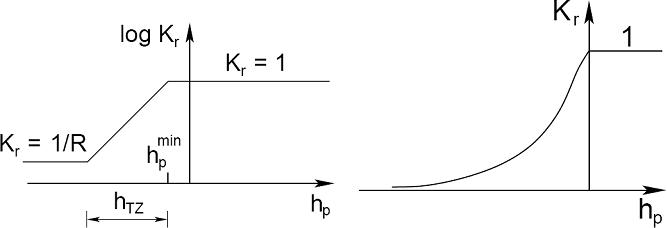(a) Log-lineární model [1], (b) Van Genuchtenův model [2]
Log-lineární model
Log-lineární model přechodové vrstvy je popsán např. v [1,3] a je definován následujícími parametry:
hpmin | - | minimální hodnota tlakové výšky v plně nasyceném prostředí [kPa] | |
hTZ | - | šířka přechodové zóny [m] | |
R | - | parametr redukce, obecně velké číslo R = 100 až 1000 [-], defaultní nastavení předpokládá R = 1000 [-] |
Součinitel relativní permeability Kr je dán výrazem:
Gardnerův model
Jedná se o ekvivalentní model závislý pouze na jednom parametru α [1/m]. Součinitel relativní permeability Kr je v tomto případě dán výrazem [4]:
Van Genuchtenův model
V tomto případě je hodnota součinitele relativní permeability Kr dána výrazem:
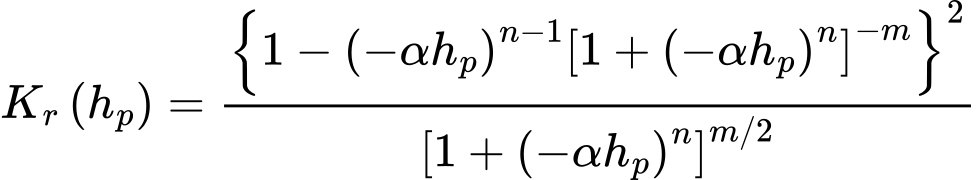
kde α [1/m], n > 1, m = 1-1/n jsou parametry modelu, jejichž hodnoty lze určit z laboratorních měření retenčních křivek aproximované vztahem:
kde: | Ssat | - | stupeň nasycení při plné saturaci, standardní nastavené Ssat = 1 |
Sr | - | reziduální stupeň nasycení | |
Θ | - | normalizovaný obsah vody |
Parametr Θ je obecně dán výrazem:
kde: | θr | - | reziduální obsah vody [m3/m3] |
θS | - | obsah vody při plném nasycení [m3/m3] |
Aktuální stupeň nasycení S lze vyjádřit v závislosti na obsahu vody θ a pórovitosti zeminy n následovně (je nutné rozlišovat n vyjadřující pórovitost a n, které vystupuje ve van Genuchtenově modelu, jedná se o dvě různé veličiny):
V případě Log-lineárního a Gardnerova modelu je použita zjednodušená forma van Genuchtenova modelu podle [5]:
kde parametr b > 0 [-] zavádíme pro lepší zachycení retenčních vlastností dané zeminy.
Doporučuji následující tabulky parametrů, které skutečně zadáváme. Parametry jsou přepočítány na základě hodnot uvedených v originálních tabulkách.
Orientační hodnoty parametrů van Genuchtenova modelu pro různé způsoby zatřídění podle zrnitostní třídy USDA a FAO uvádějí následující tabulky.
Tabulka s regresními koeficienty pro zrnitostní třídy USDA podle Van Genuchtena (1991)
Zemina (zrnitostní třída) | Ksat [m/den] | RETC | Rosetta | ||||||
e [-] | Sr [-] | α [1/m] | n [-] | e [-] | Sr [-] | α [1/m] | n [-] | ||
Písek | 7,13 | 0,75 | 0,11 | 14,5 | 2,68 | 0,60 | 0,14 | 3,5 | 3,18 |
Hlinitopísčitá | 3,50 | 0,70 | 0,14 | 12,4 | 2,28 | 0,64 | 0,13 | 3,5 | 1,747 |
Písčitohlinitá | 1,06 | 0,70 | 0,16 | 7,5 | 1,89 | 0,63 | 0,10 | 2,7 | 1,448 |
Hlinitá | 0,25 | 0,75 | 0,18 | 3,6 | 1,56 | 0,66 | 0,15 | 1,1 | 1,474 |
Jemný písek | 0,06 | 0,85 | 0,07 | 1,6 | 1,37 | 0,96 | 0,10 | 0,7 | 1,677 |
Prachovitá hlína | 0,11 | 0,82 | 0,15 | 2,0 | 1,41 | 0,78 | 0,15 | 0,5 | 1,663 |
Písčitá jílovitohlinitá | 0,314 | 0,64 | 0,26 | 5,9 | 1,48 | 0,62 | 0,16 | 2,1 | 1,33 |
Jílovitohlinitá | 0,062 | 0,70 | 0,23 | 1,9 | 1,31 | 0,79 | 0,18 | 1,6 | 1,415 |
Prachovitá jílovitohlinitá | 0,017 | 0,75 | 0,21 | 1,0 | 1,23 | 0,93 | 0,19 | 0,8 | 1,52 |
Písčitý jíl | 0,029 | 0,61 | 0,26 | 2,7 | 1,23 | 0,63 | 0,30 | 3,3 | 1,207 |
Prachovitý jíl | 0,0048 | 0,56 | 0,19 | 0,5 | 1,09 | 0,93 | 0,23 | 1,6 | 1,321 |
Jíl | 0,048 | 0,61 | 0,18 | 0,8 | 1,09 | 0,85 | 0,21 | 1,5 | 1,253 |
Tabulka s regresními koeficienty pro 11 zrnitostních tříd FAO podle Van Genuchtena (1998)
Zemina (zrnitostní třída) | Ksat [m/den] | e [-] | Sr [-] | α [1/m] | n [-] |
Povrchová zemina (do hloubky 1 m) | |||||
Hrubozrnná (C) | 0,600 | 0,68 | 0,062 | 3,83 | 1,3774 |
Střednězrnná (M) | 0,121 | 0,78 | 0,023 | 3,14 | 1,1804 |
Středně jemnozrnná (MF) | 0,023 | 0,75 | 0,023 | 0,83 | 1,2539 |
Jemnozrnná (F) | 0,248 | 1,08 | 0,019 | 3,67 | 1,0120 |
Velmi jemnozrnná (VF) | 0,150 | 0,78 | 0,016 | 2,65 | 1,1033 |
Zemina v hloubce (> 1 m) | |||||
Hrubozrnná (C) | 0,700 | 0,58 | 0,068 | 4,30 | 1,5206 |
Střednězrnná (M) | 0,108 | 0,65 | 0,026 | 2,49 | 1,1689 |
Středně jemnozrnná (MF) | 0,040 | 0,70 | 0,024 | 0,82 | 1,2179 |
Jemnozrnná (F) | 0,085 | 0,93 | 0,021 | 1,98 | 1,0861 |
Velmi jemnozrnná (VF) | 0,082 | 1,17 | 0,019 | 1,68 | 1,0730 |
Tabulka : Klasifikační systém textury zemin FAO
Zemina | Definice |
Hrubozrnná (C) Střednězrnná (M) | jíl < 18% a písek > 65% 18%< jíl < 35% a 15%< písek nebo: jíl < 18% a 15%< písek < 65% |
Středně jemnozrnná (MF) | jíl < 35% a písek < 15% |
Jemnozrnná (F) | 35%< jíl < 60% |
Velmi jemnozrnná (VF) | 60%< jíl |
Literatura:
Podrobné informace jsou dostupné v [2].
[1] D.M. Potts, L. Zdravkovič, Finite element analysis in geotechnical engineering - theory, Thomas Telford, London, 1999.
[2] M. Th. Van Genuchten, A closed formulation for predicting the hydraulic conductivity of unsaturated soils, Journal Soil Science Society of America 44, 239-259, 1988..
[3] M. Šejnoha, Finite element analysis in geotechnical design, to appear (2015)
[4] W. R. Gardner, Some steady-state solutions of the unsaturated moisture flow equation to evaporation from a water table, Soil Science 85(4), 228-232, 1958.
[5] M. Šejnoha, T. Janda, H. Pruška, M. Brouček, Metoda konečných prvků v geomechanice: Teoretické základy a inženýrské aplikace, předpokládaný rok vydání (2015)
[6] USDA 1951. Soil Survey Manual. Soil Conservation Service. U.S. Department of Agriculture Handbook No. 18. US Government Printing Office. Washington DC.
[7] Wösten, J.H.M., et. al. 1998. Using existing soil data to derive hydraulic parameters for simulation models in environmental studies and in land use planning. Final Report on the European Union Funded project. DLO Winand Staring Centre. Report 156, Wageningen, NL. p. 106. ISSN 0927-04537.