Spencer
Spencerova metoda je obecná proužková metoda mezní rovnováhy. Je založena na splnění rovnováhy sil i momentů na jednotlivých blocích. Bloky vzniknou rozdělením oblasti zeminy nad smykovou plochou dělicími rovinami. Statické schéma bloků a sil, které na ně působí, je zachyceno na obrázku:
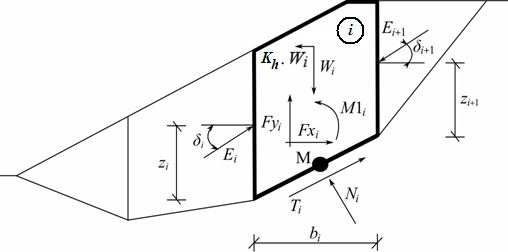 Statické schéma - Spencerova metoda
Statické schéma - Spencerova metoda
U každého bloku se předpokládá působení následujících sil:
Wi | - | tíha bloku, včetně přitížení, které má charakter tíhy (hmotné) a včetně vlivu součinitele vertikálního zemětřesení Kv |
Kh*Wi | - | vodorovná setrvačná síla modelující účinky zemětřesení, Kh je faktor vodorovného zrychlení při zemětřesení |
Ni | - | normálová síla na smykové ploše |
Ti | - | smyková síla na smykové ploše |
Ei, Ei+1 | - | síly, jimiž na sebe působí sousední bloky, jsou odkloněny od vodorovné o úhel δ |
Fxi,Fyi | - | ostatní vodorovné a svislé síly působící na blok |
M1i | - | moment od sil Fxi, Fyi otáčející kolem bodu M, což je střed i-tého úseku smykové plochy |
Ui | - | výslednice pórového tlaku na i-tém úseku smykové plochy |
Pro výpočet limitní rovnováhy sil a momentů na blocích jsou ve Spencerově metodě zavedeny následující předpoklady:
- dělicí plochy mezi bloky jsou vždy svislé
- paprsek tíhy bloku Wi prochází středem i-tého úseku smykové plochy, bodem M
- normálová síla Ni působí ve středu i-tého úseku smykové plochy, v bodě M
- sklon meziblokových sil Ei je konstantní pro všechny bloky a má hodnotu δ, jen na počátku a na konci smykové plochy je δ = 0
Řešení vychází z následujících vztahů:
![]()
![]()
![]()
![]()
![]()
kde: | φi | - | úhel vnitřního tření zeminy na úseku smykové plochy |
ci | - | soudržnost zeminy na úseku smykové plochy | |
αi | - | sklon úseku smykové plochy |
Rovnice (1) je vztah mezi efektivní a totální hodnotou normálové síly na smykové ploše. Rovnice (2) je Mohr-Coulombova rovnice vyjadřující vztah mezi normálovou a smykovou sílou na úseku smykové plochy. Rovnice (3) je součtová výminka ve směru kolmém k i-tému úseku smykové plochy, rovnice (4) je součtová výminka ve směru i-tého úseku smykové plochy. SF je stupeň stability svahu, kterým jsou redukovány parametry zemin. Rovnice (5) je momentová výminka k bodu M, v níž ygi je svislá souřadnice působiště tíhy bloku a yM je svislá souřadnice bodu M.
Úpravou rovnic (3) a (4) je získán rekurentní vztah:
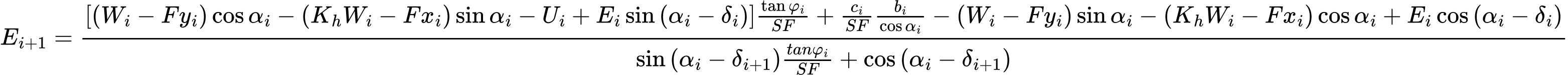
Z tohoto vztahu lze pro dané hodnoty δ a SF postupně dopočítat všechny meziblokové síly E, vycházejíce z faktu, že na počátku smykové plochy je hodnota E známá, a to E1 = 0.
Z momentové výminky (5) je získán další rekurentní vztah:
![]()
Z tohoto vztahu se pro danou hodnotu δ určí všechna ramena meziblokových sil z, při známé hodnotě vlevo na počátku smykové plochy, kde z1 = 0.
Výpočet stupně stability SF probíhá dvojnásobným iteračním postupem s následujícími kroky:
- Zvolí se prvotní hodnota úhlu δ, a to δ = 0.
- Pro danou hodnotu δ se ze vztahu (6) stanoví odpovídající stupeň stability SF, a to tak, že na horním konci smykové plochy musí být hodnota En+1 = 0.
- Pro hodnoty sil E stanovené v předchozím kroku se ze vztahu (7) vypočítá velikost úhlu δ, a to tak, aby na posledním bloku vpravo vyšla nulová hodnota momentu. Vztah (7) už neurčuje hodnotu zn+1, ta je totiž nulová. Při této nulové hodnotě zde musí být splněna momentová výminka (5).
- Iterace končí tehdy, pokud se úhel δ dalším opakováním kroku 2 a 3 nemění.
Aby proces iterace probíhal pokud možno stabilně, je třeba se vyhnout oblasti nestabilit řešení. K těmto nestabilitám dochází v těch bodech, kde při vyčíslování vztahů (6) a (7) dochází k dělení nulou. Ve vztahu (7) dochází k dělení nulou tehdy, je-li δ = π/2 nebo δ = -π/2. Proto hodnota úhlu δ musí ležet v intervalu (-π/2; π/2).
Ve vztahu (6) dochází k dělení nulou tehdy, platí-li:
![]()
Další ošetření případné numerické nestability spočívá v kontrole velikosti parametru mα. Musí být splněna následující podmínka:
![]()
Proto je před začátkem iterace nutné nalézt nejvyšší z kritických hodnot SFmin splňujících výše uvedené podmínky. Hodnoty ležící níže než je tato kritická hranice SFmin se vyskytují v oblasti nestabilit řešení, proto iterace začíná nastavením SF na hodnotu "těsně" nad SFmin a všechny výsledné hodnoty SF vystupující v iteraci jsou větší než SFmin.
Obecně lze říci, že rigorózní metody konvergují hůře než metody jednodušší (Bishop, Fellenius). Příklady vykazující problémy s konvergencí zahrnují např. příliš strmé úseky smykové plochy, složitou geometrii, výrazný skokový nárůst přitížení atd. Pokud metoda nespočte výsledek, doporučujeme lehce změnit zadání, např. zadat méně strmou plochu, vložit více bodů do smykové plochy atd., příp. pro výpočet použít některou z jednodušších metod.
Literatura:
Spencer, E. 1967. A method of analysis of the stability of embankments assuming parallel interslice forces. Géotechnique, 17(1): 11-26.