Achsensymmetrie
Dieses Berechnungsmodul eignet sich zur Lösung von rotationssymmetrischen Problemen. Sowohl die geometrische Anordnung der Konstruktion als auch die Belastung müssen diese Anforderung erfüllen. Ein geeignetes Beispiel ist die Lösung eines vertikal belasteten Einzelpfahls, eines kreisförmigen Grabens oder die Grundwasserentnahme aus der kreisförmigen Bohrung.
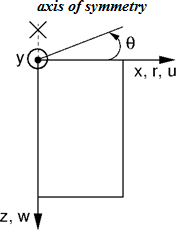Achsensymmetrische Berechnung
Wie beim Problem der ebenen Verformung handelt es sich in der Regel um ein dreidimensionales Problem, das jedoch wieder in eine planare Problemlösung umgewandelt werden kann (siehe Abb.). Die Lösung bezieht sich dann auf 1 m Bogenlänge mit dem Radius x(r). Die Symmetrieachse repräsentiert immer den Ursprung der x(r) -Koordinate. Scherkomponenten der Verformung in Drehrichtung können vernachlässigt werden. Zusätzlich zu den Spannungs- und Dehnungskomponenten in der Schnittebene betrachten wir auch die Entwicklung einer Umfangsnormalspannungs- und Dehnungskomponente. Die entsprechenden Nicht-Null-Spannungs- und Dehnungskomponenten können wie folgt zu einem Spannungs- und Dehnungsvektor zusammengesetzt werden:
Es ist sichtbar, dass die Umfangskomponente der Verformung und damit die betreffenden Normalspannungskomponenten an der Symmetrieachse die unendlichen Werte erreichen. Für eine genauere Bestimmung der Finite-Elemente-Methode ist ein ausreichend feines Netz um die Symmetrieachse erforderlich.
Beachten Sie die Aufbringung von Linien- und Oberflächenlasten. In der folgenden Abbildung sind einige Beispiele für die Belastung der Geländeoberfläche dargestellt. Offensichtlich nimmt der Einfluss dieser Belastungen mit dem Abstand von der Symmetrieachse zu. Daher wird das Aufbringen dieser Belastungstyp direkt auf die Symmetrieachse nicht in die Berechnung einbezogen. In diesem Fall muss die Belastungsart der Symmetrieachse gewählt werden. Das Programm erlaubt nur die konzentrierte Punktbelastung.
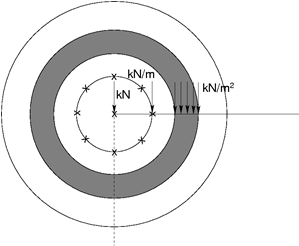Beispiele von Geländeauflast
Im Fall der Balkenelementen handelt es sich um eine Lösung einer ebenen rotationssymmetrischen Membran unter dem Einfluss von Biegeeffekten. Die Freiheitsgrade ungleich Null sind identisch mit dem Beispiel des Plattenstreifens, das zur Lösung des Problems der ebenen Deformation herangezogen wird. Neben den axialen (Meridian-) Einflüssen sind auch Membran- und Biegeeffekte in Umfangsrichtung zu berücksichtigen (siehe folgende Abbildung).
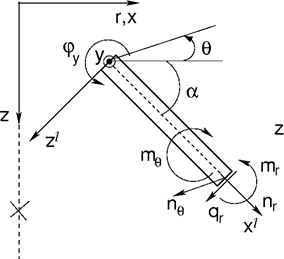Balkenelement in der Achsensymmetrie
Die jeweiligen Komponenten der inneren Kräfte (siehe Abb.), bezogen auf 1 m Breite, können wie folgt zu einem Spannungsvektor zusammengesetzt werden:
Im Fall der Kreisplatten oder Kreisringen (Winkel α = 0) kann von radialen und Umfangskomponenten der inneren Kräfte gesprochen werden (siehe folgende Abbildung).
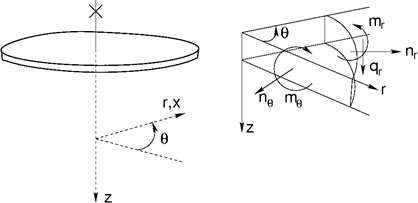Innere Kräfte auf der Kreisplatte
Die Beziehung zwischen den inneren Kräften und den jeweiligen Verformungskomponenten kann allgemein in folgender Form eingetragen werden:
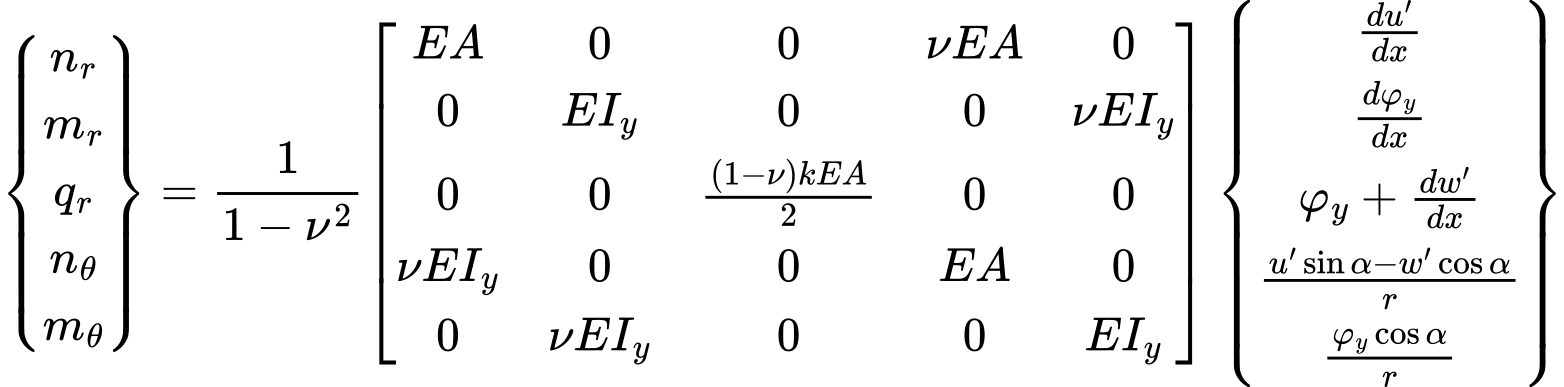
Wenn wir den Querschnitt r auf unendlich setzen, kommen wir zum Problem der ebenen Deformation. Es ist anzumerken, dass im Fall der Scherkräften ihr Wert im Gegensatz zum Problem der ebenen Deformation, stark von der Dichte der Teilung des Balkens an die Elemente abhängt. Dies gilt auch für vertikale Reaktionen.
Hinweis zur Strömung
Es ist zu bemerken, dass ähnlich wie die Reaktion bei der Spannungsberechnung Werte der Punktströmung an Netzknoten mit vorgeschriebenen Porendrücken auf 1 m Bogenlänge mit dem Radius x(r). bezogen sind. Im Fall der ebener Deformation beziehen sich die jeweiligen Werte der Punktströmungen auf 1 m der Länge. Dies entspricht den Gesamtdurchfluss-Werten, die sich aus Punktströmungen [m3/Tag/m] wie folgt ermitteln lassen:
Ebene Deformation
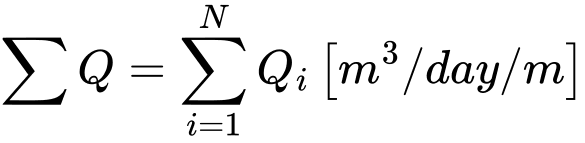
Achsensymmetrie
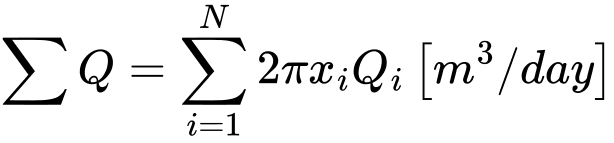
wo N die Anzahl der Knoten der jeweiligen Netzlinie, in denen die Punktströmung Qi [m3/Tag/m]. berechnet werden. Im Fall der Achsensymmetrie ist xi der Wert der x-Koordinate des gegebenen Punktes. Es handelt sich also um den Gesamtdurchfluss [m3/Tag] beispielsweise durch eine Zylinderfläche (vertikale Linie) oder eine Kreisfläche (horizontale Linie).