Koordinatensystem (Zeichenkonvention)
Innere Kräfte
Innere Kräfte werden nachfolgend definiert:
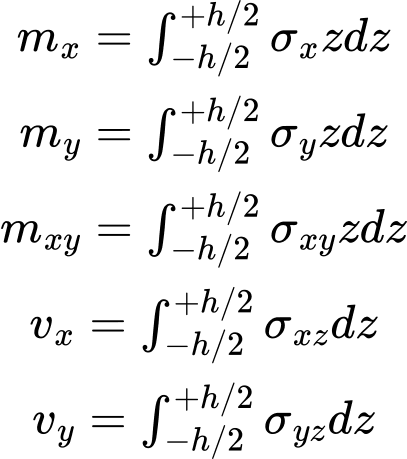
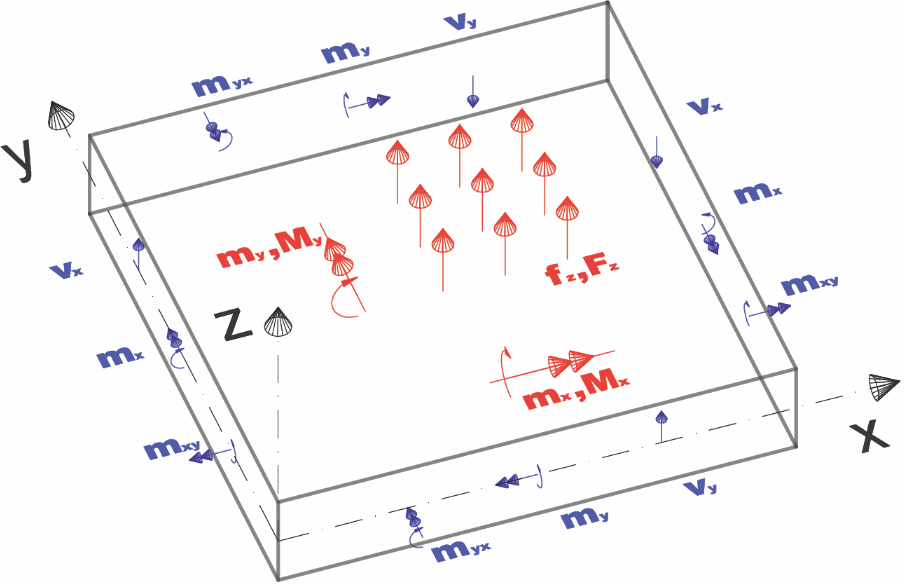
Die positive Richtung der Schnittgrößen ist aus der folgenden Abbildung ersichtlich:
Die Hauptmomente und die Richtung der Hauptachsen werden anhand der folgenden Formeln berechnet:
![]()
![]()
Der Sinn dieser Variablen lautet wie folgt: innere Kräfte können vom Koordinatensystem (x, y) in ein anderes System (x´, y´) umgewandelt werden, das durch Drehung um die z-Achse um einen bestimmten Winkel erzeugt wird. Der Winkel α ist ein solcher Drehwinkel, dass das transformierte Moment mx´y´ gleich Null ist und die Momente mx´ und my´ Maximal- bzw. Mindestwerte von m1 und m2 erreichen.
Ähnlich wird die maximale Scherkraft bestimmt:
![]()
und der Winkel zwischen vmax und der x-Achse:
![]()
Belastung
Die Konvention der Eingabe von Kraft- und Momentbelastung ergibt sich aus der folgenden Abbildung:
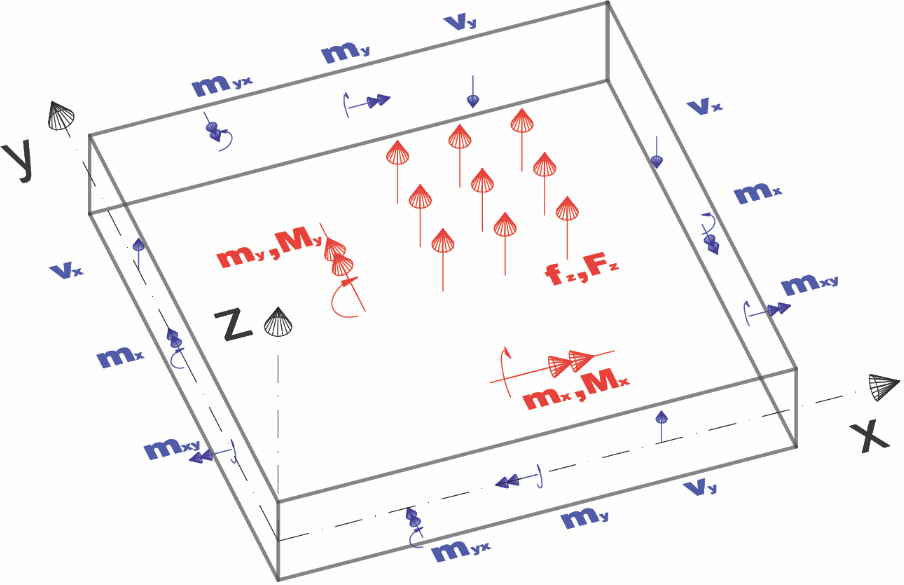
Wir machen aufmerksam auf die unterschiedliche Konvention bei der Eingabe der Momentbelastung M (an einem Punkt oder entlang der Linie) und der inneren Momente m. Während sich das Moment Mx um die x-Achse dreht (wie es für Balken üblich ist), ist die innere Kraft, die sich um x dreht my.