Drucker-Prager
The Drucker-Prager material model is the most simple material model, which can be adopted for the modeling of a nonlinear response of soils. Unlike the Mohr-Coulomb model, the Drucker-Prager yield surface is smooth and in the principal stress space plots as a cylindric cone. As evident from the figure below, the yield surface, similarly to the Mohr-Coulomb model, depends on the mean effective stress σmeff. The current version of the model implemented in GEO5 FEM grounds on the assumption of triaxial extension. In other words, the projection of the yield surface fDP into a deviatoric plane passes through internal vertexes of the Mohr-Coulomb hexagon, θ = - 30°, where θ is the Lode angle.
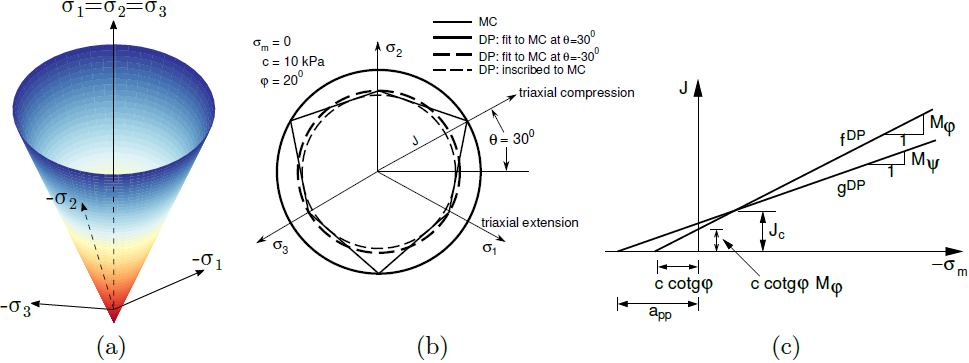 a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
The Drucker-Prager model allows for taking into account the material dilatancy (evolution of positive volumetric plastic strains during plastic shearing) by introducing the dilatancy angle ψ. Evolution of plastic strains is in general controlled by the plastic potential gDP. While the slope of the yield surface in the meridian plane is given by the angle of internal friction Mφ = Mφ(φ), the slope of the plastic potential surface depends on the dilatancy angle Mψ = Mψ(ψ). The condition ψ = φ corresponds to the associated flow rule, otherwise the non-associated flow rule is considered. Further details can be found in the theoretical manual. Because the soil eventually arrives at so called critical state (zero increment of the volumetric plastic strain during plastic shearing), it is desirable to limit the extent of dilation. This requires introduction of the maximum void ratio emax, for which reaching the critical state ψ = 0 is expected. An illustrative example is presented here. How the choice of the value of dilatancy angle influences the prediction of the soil response in comparison to its real behavior is presented here. For the sake of clarity we present, on the following figure, a graphical representation of the evolution of the volumetric strain with dilation cutoff.
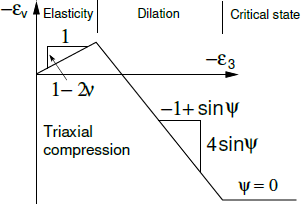 Evolution of volumetric plastic strain with dilation cutoff
Evolution of volumetric plastic strain with dilation cutoff
The basic material parameters defining the Drucker-Prager model are listed in the following table. These parameters can be adopted when performing analysis under drained conditions or in the case of undrained conditions, Type (1): analysis in effective stresses (cef, φef). When choosing the Type (2): analysis in effective stresses (Su) the value of effective cohesion c is replaced by the value of undrained shear strength Su. The value of the effective angle of internal friction φ = φu is set to zero, φ = 0. The Drucker-Prager yield surface is then replaced by the Mises yield surface, see below. However, the stiffness parameters are assumed effective. With undrained conditions it is generally expected that the soil does not experience dilation. The dilation angle ψ = 0 is therefore adopted for both options.
It is evident from the table of material parameters that the Drucker-Prager model, similarly to the Modified elastic model, considers a different soil response in primary loading and in unloading/reloading by introducing the unloading/reloading modulus Eur, see also the Mohr-Coulomb model.
Symbol | Units | Description | |
| [MPa] | Modulus of elasticity | |
| [MPa] | Modulus of unloading/reloading | |
| [-] | Poisson's ratio | |
| [kPa] | Effective coefficient of cohesion | |
| [°] | Effective angle of internal friction | |
| [°] | Dilatancy angle | |
| [kN/m3] | Bulk weight | |
| [-] | Initial void ratio corresponding to the state at the end of 1st calculation stage | |
| [-] | Maximum void ratio to terminate dilation (when limiting dilation) | |
| [1/K] | Coefficient of thermal expansion (when considering temperature effects) |
When choosing undrained conditions Type (3): analysis in total stresses Su the Drucker-Prager yield surface is again replaced by the Mises yield surface. Similarly, the Mohr-Coulomb yield surface is replaced by the Tresca yield surface. A graphical representation is provided in the figure. This option thus considers φ = ψ = 0, which corresponds to the associated flow rule. Since modeling a volumetrically incompressible material, the value of Poisson's ratio is typically selected in the range of (0.49 - 0.499). Point out that setting the value of Poisson's ratio too close to 0.5 may result in numerical instabilities. At best case the results will be quite inaccurate. Further information can be found in the theoretical manual.
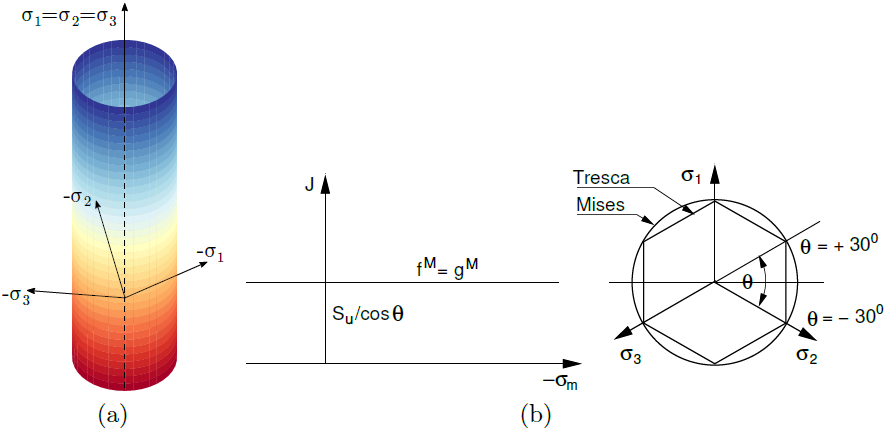 a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
The material parameters defining the Mises of Tresca yield surface are available in the following table. In the case of Mises yield surface the value of Lode angle θ is constant equal to θ = ± 30°.
Symbol | Units | Description | |
Eu | [Pa] | Undrained modulus of elasticity | |
Su | [Pa] | Undrained shear strength | |
ν | [-] | Poisson's ratio assumed in the range of (0.49 - 0.499) | |
γ | [kN/m3] | Bulk weight | |
α | [1/K] | Coefficient of thermal expansion (when considering temperature effects) |
The Drucker-Prager model allows, similarly to the Mohr-Coulomb model, for performing the stability analysis. Both the standard slope stability analysis and stability analysis within a given construction stage can be carried out. In both cases, this task is solved by gradually reducing the shear strength parameters c, φ by introducing the reduction parameter ζ such that
![]()
where c, φ are the actual shear strength parameters and cd, φd are the reduced parameters. The Factor of safety FS is then given by
![]()
Similarly we reduce the dilatancy angle ψ providing ψ ≠ 0.
Implementation of the Drucker-Prager material model into the GEO5 FEM program is described in detail in the theoretical manual.