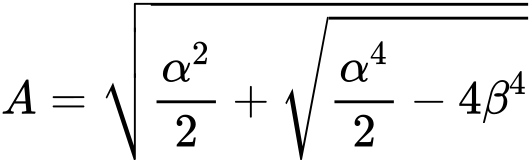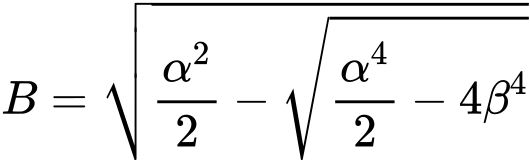Geometrische Methode (Euler)
Der Boden um den Mikropfahl herum wird im Programm durch Bettungsmodul Ep (Winkler-Konstante k) modelliert, das vom Benutzer im Fenster "Berechnung Querschnitt" eingegeben wird. Das Konstruktionsmodell wird in der Abbildung dargestellt.
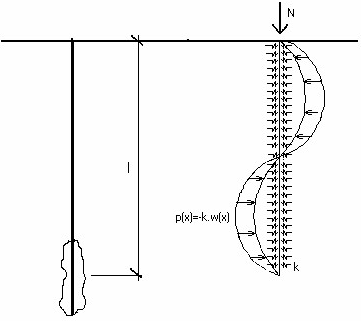Konstruktionsmodell
Bei dem Druckmikropfahl wird abhängig von der Geometrie bzw. der Steifigkeit der Konstruktion variable Anzahl von Halbwellen vorausgesetzt. Die Lösung für diesen Fall basiert auf der Biegungsgleichung von direkter Stab.
Nach der Bearbeitung kann die Biegungsgleichung nachfolgend ausgedrückt werden:
| |
wo: | |
| |
| |
| |
|
Für die Berechnung von C1-C4-Integrationskonstanten werden vier Randbedingungen verwendet, die Art der Lagerung der Endpunkten zeichnen.
Die Größe der kritischen Kraft Ncr lässt sich mit einer aus der Elastizitätstheorie bekannten allgemeinen Beziehung berechnen (siehe Literatur [1]):
wo: | Ei | - | Elastizitätsmodul des idealen Querschnitts |
Ii | - | Trägheitsmoment des idealen Querschnitts | |
lp | - | effektive Mikropfahllänge (freie Mikropfahllänge + 1/2 der Wurzellänge) | |
Ep | - | ||
n | - | Anzahl der Halbwellen der Biegelinie entlang der Länge des Mikropfahls |
Als Minimum der Funktion (1) wird die kritische Kraft Ncr gesucht. Dies wird für die Länge der Halbwelle erreicht
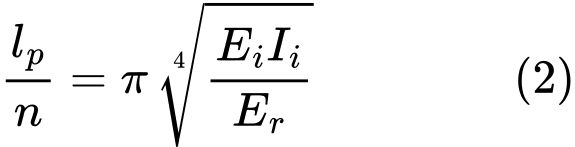
Gleichung (2) gibt die Beziehung für die Anzahl der Halbwellen an n:
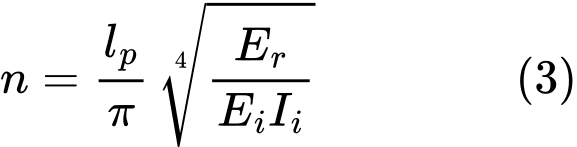
Befindet sich der Mikropfahl teilweise über dem Boden (versetzt), werden die reduzierten Werte von n und Er in Bezug auf die Länge des Mikropfahls über dem Boden bestimmt:
wo: | lv | - | Länge des Mikropfahls über dem Gelände |
Für die Einbettung des Mikropfahls "Gelenk-Gelenk" wird die kritische Kraft Ncr aus der Beziehung bestimmt:
Für die Einbettung des Mikropfahls "Gelenk-Einspannung" wird die kritische Kraft Ncr aus der Beziehung bestimmt:
Literatur:
[1] Timoshenko, S. P.: Theory of Elastic Stability, New York, 1936