Kreisförmige Gleitfläche
Alle Methoden der Grenzgleichgewichts-Zustände gehen davon aus, dass der Erdkörper über der Kreisgleitfläche in Blöcke (Lamellen) unterteilt ist (die Teilungsebenen zwischen der Blöcke sind immer vertikal). Die Kräfte, die auf individuelle Blöcke wirken, sind in der Abbildung dargestellt:
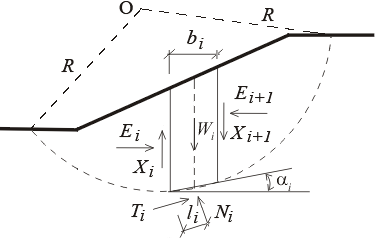 Statisches Schema - Bishop Methode
Statisches Schema - Bishop Methode
In diesem Fall sind Xi und Ei die Scher- und Normalkräfte, die zwischen den Blöcken wirken, Ti und Ni die Scher- und Normalkräfte, die auf einzelne Segmente der Gleitfläche wirken, Wi sind die Gewichte der einzelnen Blöcke.
Die einzelnen Gleitflächenmethoden unterscheiden sich in ihren Annahmen zur Erfüllung der Kraftbedingungen des Gleichgewichts und der Momentenbedingungen um den Mittelpunkt O.
Das Programm erlaubt die Berechnung mit folgenden Lamellenverfahren:
Wenn im Böschungsschnitt die Grundwasser eingegeben ist (eine von fünf Möglichkeiten), wird es die Blockgewichtsberechnung und der Berechnung der Scherkräfte (durch Zählen des Porendrucks) beeinflussen. In die Beziehungen zwischen der Normal- und Scherkräften werden effektive Scherparameter der Bodenfestigkeit zuzuordnen.
Ankerkräfte und Wasser über dem Gelände in die Berechnung mit einbeziehen:
Ankerkräfte werden als externe Lasten, die auf die Böschung wirken, betrachtet. Sie werden bezüglich eines laufenden Meters der Böschung [kN/m] betrachtet und in die Momentengleichung mit einbezogen. Diese Kräfte sollen für zusätzliche Stabilität sorgen, falls dies nicht auf andere Weise erreich werden kann. Es gibt keine Grenzen für die Größe der Ankerkräfte, deswegen ist es wichtig, mit realistischen Werten zu arbeiten.
Der Einfluss von Wasser oberhalb der Geländeoberfläche wird als senkrecht wirkende Kraft auf die Geländeoberfläche sowie Porenwasserdruck entlang der Gleitfläche, welcher abhängig von der Tiefe der Gleitfläche, vom Grundwasserspiegel aus gemessen, ist. Die Kräfte, die auf die Geländeoberfläche wirken, gehen in das Momentengleichgewicht als Kräfte, die auf den jeweiligen Teil in Richtung der Gleitfläche wirken.
Die Optimierung der kreisförmigen Gleitfläche sucht nach der kritischsten Fläche (niedrigster SF).