Linienlast - Aktiver Erddruck
Die unendlich lange verteilte Last f, die parallel zur Konstruktion auf die Bodenoberfläche wirkt, führt zu einer dreieckigen Erhöhung des aktiven Erddrucks, der auf die Konstruktion über einen bestimmten Abschnitt hf angewendet wird - siehe Abbildung:
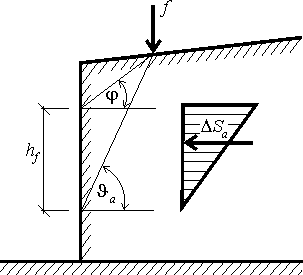 Schema der Zunahme des aktiven Erddrucks durch vertikale Linienlast, die auf die Bodenoberfläche wirkt
Schema der Zunahme des aktiven Erddrucks durch vertikale Linienlast, die auf die Bodenoberfläche wirkt
Der Bereich des Erddruckeinflusses wird durch zwei von den Endpunkten der verteilten Last gezogene Linien mit dem Winkel φ und dem Winkel ϑa (entsprechend der kritischen Gleitfläche) bestimmt, der gegeben ist zu:
![]()
wo: | φ | - | Winkel der inneren Reibung des Bodens |
ε | - | Winkel, durch der folgenden Formeln ermittelt |
![]()
![]()
![]()
wo: | β | - | Böschungsneigung |
φ | - | Winkel der inneren Reibung des Bodens | |
δ | - | Reibungswinkel zwischen Konstruktion und Boden | |
α | - | rückseitige Neigung der Konstruktion | |
c | - | Kohäsion des Bodens | |
γ | - | Wichte des Bodens | |
h | - | angenommene Tiefe |
Für nicht-homogenen Boden und einer Neigung der Bodenfläche β kleiner als der Winkel der inneren Reibung der Bodens φ, ist der Winkel ε gegeben durch:
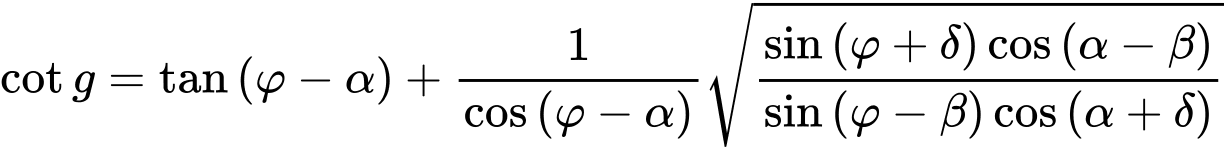
wo: | β | - | Böschungsneigung |
φ | - | Winkel der inneren Reibung des Bodens | |
δ | - | Reibungswinkel zwischen Konstruktion und Boden | |
α | - | rückseitige Neigung der Konstruktion |
Das Ergebnis der Erhöhung des aktiven Erddrucks aufgrund der Linienlast f ist gegeben durch:
![]()
wo: | ϑa | - | Winkel der kritischen Gleitfläche |
φ | - | Winkel der inneren Reibung des Bodens | |
δ | - | Reibungswinkel zwischen Konstruktion und Boden | |
f | - | Größe der Linienlast |
Für nicht-homogene Böden geht das Programm wie folgt vor.