Materialmodell der Strömung
Die Beziehung zwischen Strömungsgeschwindigkeit und Änderung der hydraulischen Höhe (Porendruck) wird durch das Darcy-Gesetz bestimmt. Die aktuelle Version geht von konstanten Werten der Filterkoeffizienten aus. Die Abhängigkeit zwischen Filtrationskoeffizienten und Porendruck wird nicht berücksichtigt.
Weiterhin wird als nächstes die anfängliche Porenzahl des Bodens e0 ein, um die tatsächliche Bodenporosität n und dann die tatsächliche Strömungsgeschwindigkeit der Flüssigkeit, die nur durch die Poren vs=v/n fließt, zu bestimmen, wobei v die durchschnittliche Geschwindigkeit in der gesamten Durchlässigkeitsfläche ist. Im Allgemeinen die Porenzahl e0 = 1 entspricht der Bodenporosität n = 50%..
Durch die Eingabe von Koeffizient der relativen Permeabilität Kr kann der Übergang zwischen der vollständig gesättigten (S = 1,Kr = 1) und der ungesättigten (Kr => 0) Umgebung überwacht werden. Ein Beispiel ist die Lösung des Problems der stabilen Strömung mit freier Wasserfläche. Der Übergang zwischen einer vollständig gesättigten und einer ungesättigten Umgebung kann durch eines von drei Modellen zur Entwicklung des Koeffizienten der relativen Permeabilität Kr abhängig vom Wert des Porendrucks und der Druckhöhe gesteuert werden, siehe Abbildungen.
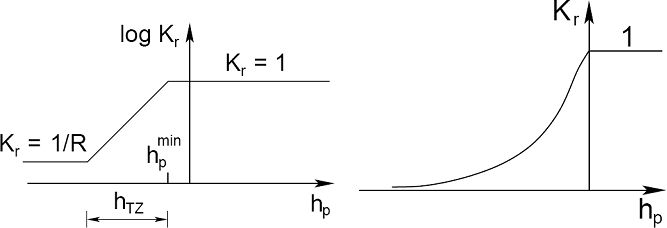 (a) Log-lineares Modell [1], (b) Van-Genuchten-Modell [2]
(a) Log-lineares Modell [1], (b) Van-Genuchten-Modell [2]
Log-lineares Modell
Das Log-lineare Modell der Übergangsschicht ist z. B. in [1,3] beschrieben und wird durch folgende Parameter definiert:
hpmin | - | der minimalen Wert der Druckhöhe in der voll gesättigten Umgebung [kPa] | |
hTZ | - | Übergangszonenbreite [m] | |
R | - | Reduktionsparameter, im Allgemeinen große Zahl R = 100 bis 1000 [-], Standardeinstellung wird vorausgesetzt von R = 1000 [-] |
Der Koeffizient der relativen Permeabilität Kr ist gegeben durch:
![]()
Gardner-Modell
Es handelt sich um ein äquivalentes Modell, das nur von einem Parameter α [1/m] abhängt. Der Koeffizient des relativen Permeabilität Kr ist in diesem Fall gegeben durch [4]:
![]()
Van-Genuchten-Modell
In diesem Fall ist der Wert des Koeffizienten der relativen Permeabilität Kr gegeben durch:
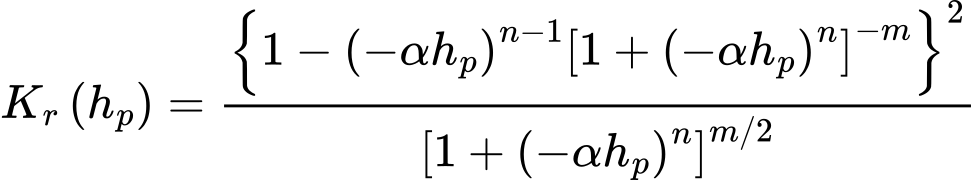
wobei α [1/m], n > 1, m = 1-1/n Modellparameter sind, deren Werte aus Labormessungen von Retentionskurven bestimmt werden können, die angenähert sind durch:
![]()
![]()
wo: | Ssat | - | Sättigungsgrad bei voller Sättigung, Standardeinstellung Ssat = 1 |
Sr | - | Restsättigungsgrad | |
Θ | - | normalisierter Wassergehalt |
Der Parameter Θ ist im Allgemeinen gegeben durch:
![]()
wo: | θr | - | Restwassergehalt [m3/m3] |
θS | - | Wassergehalt bei voller Sättigung [m3/m3] |
Der aktuelle Sättigungsgrad S kann in der Abhängigkeit vom Wassergehalt θ und der Porosität des Bodens n wie folgt ausgedrückt werden (es ist erforderlich n, als Ausdruck der Porosität n zu unterscheiden, was im Van-Genuchten-Modell dargestellt wird; dies sind zwei verschiedene Parameter):
![]()
Im Fall des Log-Linear- und Gardner-Modells wird eine vereinfachte Form des Van-Genuchten-Modells nach [5] verwendet:
![]()
wobei der Parameter b > 0 [-] eingeführt wird, um die Retentionseigenschaften des Bodens besser zu erfassen.
Wir empfehlen die folgenden Parametertabellen, die wir tatsächlich eingeben. Die Parameter werden anhand der in den Originaltabellen angegebenen Werte neu berechnet.
Orientietungswerte der Parameter des van Genuchten-Modells für verschiedene Arten der Einteilung nach der Körnigkeit der Klasse USDA und FAO sind in den folgenden Tabellen angegeben.
Tabelle mit Regressionskoeffizienten für die Klasse der Korngröße USDA gemäß Van Genuchten (1991)
Boden (Korngröße) | Ksat [m/day] | RETC | Rosetta | ||||||
e [-] | Sr [-] | α [1/m] | n [-] | e [-] | Sr [-] | α [1/m] | n [-] | ||
Sand | 7,13 | 0,75 | 0,11 | 14,5 | 2,68 | 0,60 | 0,14 | 3,5 | 3,18 |
lehmig-sandige Böden | 3,50 | 0,70 | 0,14 | 12,4 | 2,28 | 0,64 | 0,13 | 3,5 | 1,747 |
sandig-lehmige Böden | 1,06 | 0,70 | 0,16 | 7,5 | 1,89 | 0,63 | 0,10 | 2,7 | 1,448 |
Lehmige | 0,25 | 0,75 | 0,18 | 3,6 | 1,56 | 0,66 | 0,15 | 1,1 | 1,474 |
Feinkörniger Sand | 0,06 | 0,85 | 0,07 | 1,6 | 1,37 | 0,96 | 0,10 | 0,7 | 1,677 |
Schluffiger Lehm | 0,11 | 0,82 | 0,15 | 2,0 | 1,41 | 0,78 | 0,15 | 0,5 | 1,663 |
Sandig-tonige Lehmboden | 0,314 | 0,64 | 0,26 | 5,9 | 1,48 | 0,62 | 0,16 | 2,1 | 1,33 |
Tonlehm | 0,062 | 0,70 | 0,23 | 1,9 | 1,31 | 0,79 | 0,18 | 1,6 | 1,415 |
Schluffiger Tonlehm | 0,017 | 0,75 | 0,21 | 1,0 | 1,23 | 0,93 | 0,19 | 0,8 | 1,52 |
Sandiger Ton | 0,029 | 0,61 | 0,26 | 2,7 | 1,23 | 0,63 | 0,30 | 3,3 | 1,207 |
Schluffiger Ton | 0,0048 | 0,56 | 0,19 | 0,5 | 1,09 | 0,93 | 0,23 | 1,6 | 1,321 |
Ton | 0,048 | 0,61 | 0,18 | 0,8 | 1,09 | 0,85 | 0,21 | 1,5 | 1,253 |
Tabelle mit Regressionskoeffizienten für 11 Klassen der Korngröße USDA gemäß Van Genuchten (1998)
Boden (Korngröße) | Ksat [m/Tag] | e [-] | Sr [-] | α [1/m] | n [-] |
Oberflächenboden (bis zu einer Tiefe von 1 m) | |||||
Grobkörnige (C) | 0,600 | 0,68 | 0,062 | 3,83 | 1,3774 |
Mittelkörnige (M) | 0,121 | 0,78 | 0,023 | 3,14 | 1,1804 |
Mittelfeinkörnige (MF) | 0,023 | 0,75 | 0,023 | 0,83 | 1,2539 |
Feinkörnige (F) | 0,248 | 1,08 | 0,019 | 3,67 | 1,0120 |
Sehr feinkörnige (VF) | 0,150 | 0,78 | 0,016 | 2,65 | 1,1033 |
Boden in der Tiefe (> 1 m) | |||||
Grobkörnige (C) | 0,700 | 0,58 | 0,068 | 4,30 | 1,5206 |
Mittelkörnige (M) | 0,108 | 065, | 0,026 | 2,49 | 1,1689 |
Mittelfeinkörnige (MF) | 0,040 | 0,70 | 0,024 | 0,82 | 1,2179 |
Feinkörnige (F) | 0,085 | 0,93 | 0,021 | 1,98 | 1,0861 |
Sehr feinkörnige (VF) | 0,082 | 1,17 | 0,019 | 1,68 | 1,0730 |
Tabelle: Klassifizierungssystem der FAO-Bodentextur
Boden | Definition |
Grobkörnige (C) Mittelkörnige (M) | Ton < 18% und Sand > 65% 18%< Ton < 35% und 15%< Sand oder: Ton < 18% und 15%< Sand < 65% |
Mittelfeinkörnige (MF) | Ton < 35% und Sand < 15% |
Feinkörnige (F) | 35%< Ton < 60% |
Sehr feinkörnige (VF) | 60%< Ton |
Literatur:
Detaillierte Informationen finden Sie in [2].
[1] D.M. Potts, L. Zdravkovič, Finite element analysis in geotechnical engineering - theory, Thomas Telford, London, 1999.
[2] M. Th. Van Genuchten, A closed formulation for predicting the hydraulic conductivity of unsaturated soils, Journal Soil Science Society of America 44, 239-259, 1988..
[3] M. Šejnoha, Finite element analysis in geotechnical design, to appear (2015)
[4] W. R. Gardner, Some steady-state solutions of the unsaturated moisture flow equation to evaporation from a water table, Soil Science 85(4), 228-232, 1958.
[5] M. Šejnoha, T. Janda, H. Pruška, M. Brouček, Metoda konečných prvků v geomechanice: Teoretické základy a inženýrské aplikace, předpokládaný rok vydání (2015)
[6] USDA 1951. Soil Survey Manual. Soil Conservation Service. U.S. Department of Agriculture Handbook No. 18. US Government Printing Office. Washington DC.
[7] Wösten, J.H.M., et. al. 1998. Using existing soil data to derive hydraulic parameters for simulation models in environmental studies and in land use planning. Final Report on the European Union Funded project. DLO Winand Staring Centre. Report 156, Wageningen, NL. p. 106. ISSN 0927-04537.