Passiver Erddruck- die Rankine und Mazindrani Theorie
Der passive Erddruck ist nach dieser Formel gegeben:
![]()
wo: | σz | - | vertikale geostatische Spannung |
Kp | - | Koeffizient des passiven Erddrucks gemäß Rankine | |
β | - | Böschungsneigung | |
γ | - | Wichte des Bodens | |
z | - | angenommene Tiefe | |
| - | Koeffizient des passiven Erddrucks gemäß Mazindrani |
Der Koeffizient des passiven Erddrucks Kp ist gegeben zu:
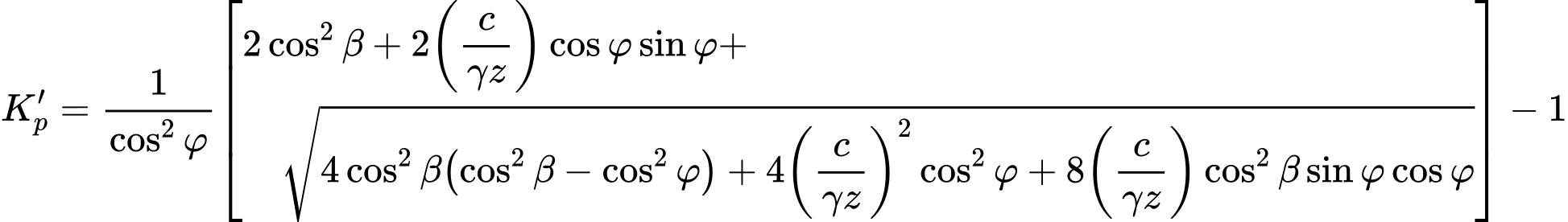
wo: | β | - | Böschungsneigung |
φ | - | Winkel der inneren Reibung des Bodens | |
c | - | Kohäsion des Bodens |
Falls keine Reibung (δ = 0) zwischen der Konstruktion und den kohäsionslosen Böden (c = 0) vorhanden ist, ist die Geländeoberfläche horizontal (β = 0) und die resultierende Gleitfläche ist auch eben mit der Böschung:
![]()
Die Mazindrani-Theorie wird dann auf die Rankine-Theorie reduziert. Der Koeffizient des passiven Erddrucks ergibt sich zu:
![]()
wo: | φ | - | Winkel der inneren Reibung des Bodens |
Der passive Erddruck σp gemäß Rankine für kohäsionslose Böden ist gegeben zu:
![]()
wo: | γ | - | Wichte des Bodens |
z | - | angenommene Tiefe | |
Kp | - | Koeffizient des passiven Erddrucks gemäß Rankine |
Literatur:
Mazindrani, Z.H., and Ganjali, M.H. 1997. Lateral earth pressure problem of cohesive backfill with inclined surface. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 123(2): 110-112.