Passiver Erddruck - die Sokolovski Theorie
Der passive Erddruck ist nach dieser Formel gegeben:
![]()
wo: | Kpg | - | Koeffizient des passiven Erddrucks für kohäsionslose Böden |
Kpc | - | Koeffizient des passiven Erddrucks aufgrund von Kohäsion | |
Kpp | - | Koeffizient des passiven Erddrucks aufgrund von Auflast | |
σz | - | vertikale normale Totalspannung |
Individuelle Ausdrücke zur Bestimmung der Größe des passiven Erddrucks und der Gleitfläche werden im Folgenden eingeführt; Die Bedeutung der einzelnen Variablen ist aus der Abbildung zu entnehmen:
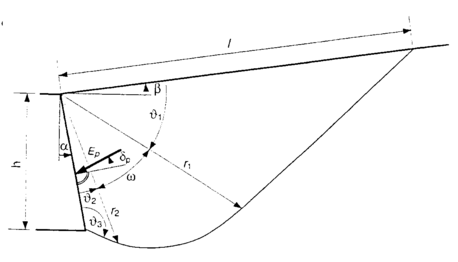 Passiver Erddruck - Gleitfläche nach Sokolovski
Passiver Erddruck - Gleitfläche nach Sokolovski
Winkel, die die Gleitfläche beschreiben:
![]()
![]()
![]()
![]()
![]()
![]()
wo: | φ | - | Winkel der inneren Reibung des Bodens |
δp | - | ||
β | - | Böschungsneigung |
Radiusvektoren der Gleitfläche:
![]()
![]()
![]()
Vorausgesetzt, dass ω < 0, überlappen die beiden geraden Kanten der Zone r1 und r2 numerisch und führen zu der im Überlappungsbereich entwickelten ebenen Gleitfläche. Die Koeffizienten des passiven Erddrucks Kpg, Kpp, Kpc folgen dann aus:
![]()
![]()
![]()
wo: | φ | - | Winkel der inneren Reibung des Bodens |
δp | - | ||
α | - | rückseitige Neigung der Konstruktion |
![]()
Hilfsvariablen: ipg, ipp, ipc, gpg, gpp, gpc, tpg, tpp, tpc
für: |
| |
|
| |
|
| |
|
| |
|
|
![]()
wo:
![]()
Für Böden mit Nullwert für den Winkel der inneren Reibung werden die folgenden Ausdrücke verwendet, um die Koeffizienten des passiven Erddrucks zu bestimmen:
![]()
![]()
wo:
![]()
![]()
![]()
![]()
Literatur:
Sokolovski, V.V., 1960. Statics of Soil Media,Butterworth, London.