Polygonale Gleitfläche
Die Lösung des Problems der Böschungsstabilität unter Annahme der polygonalen Gleitfläche basiert auf der Bestimmung des Grenzzustandes der Kräfte, die auf den Erdkörper oberhalb der Gleitfläche wirken. Um diese Kräfte einzuführen wird die Gleitfläche durch Trennflächen in Blöcke (Lamellen) unterteilt. Typischerweise sind diese Flächen vertikal, allerdings ist das keine notwendige Bedingung, z. B. werden in der Methode nach Sarma allgemein geneigten Trennflächen betrachtet.
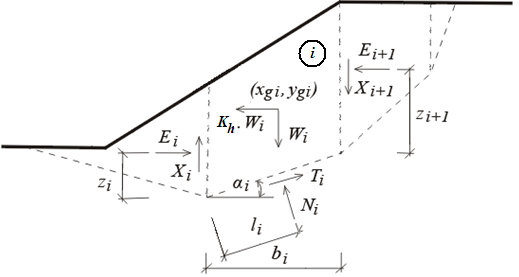 Statisches Schema eines Blocks
Statisches Schema eines Blocks
Die Abbildung zeigt die Kräfte, die auf die einzelnen Erdblöcke wirken. Falls der Bereich oberhalb der Gleitfläche in n Blöcke aufgeteilt ist, dann haben wir für die Berechnung folgenden 6n-2 Unbekannten: n Werte der Normalkräfte Ni die auf einzelne Abschnitte wirken und dazugehörige n Scherkräfte Ti; n-1 Werte der Normalkräfte Ei zwischen der Erdblöcke Ei, n-1 Werte der Normalkräfte Xi zwischen der Erdblöcke, n-1 Werte zi, die die Angriffspunkte der Kräfte Ei darstellen, n Werte li für die Angriffspunkte der Kräfte Ni und einen Stabilitätsgrad SF. Die Werte der Kräfte Xi können in manchen Methoden durch den Wert der Neigung der Kräfte Ei ersetzt werden.
Die folgenden Gleichungen sind vorhanden, um das Gleichgewichtsproblem zu lösen: n horizontale und n vertikale Gleichgewichtsgleichungen für individuelle Blöcke, n Momentengleichgewichte für individuelle Blöcke und n Beziehungen zwischen den Kräften Ni und Ti die sich auf die Blöcke nach der Theorie von Mohr-Coulomb ausbilden. Insgesamt sind es 4n Gleichungen für 6n-2 Unbekannte. Deswegen müssen 2n-2 Unbekannte im Vorhinein bestimmt werden. Die individuellen benützten Berechnungsmethoden unterscheiden sich in der Art, wie diese Werte bestimmt werden.
Meistens werden die Angriffspunkte der einzelnen Kräfte zwischen den Blöcken oder deren Neigungen ausgewählt. Um das Gleichgewichtsproblem zu lösen, wird iterativ vorgegangen, wobei die gewählten Werte sowohl für das Gleichgewicht, als auch für die kinematische Zulässigkeit der erhaltenen Lösung befriedigend sein müssen.
Das Programm kann folgende Methoden berechnen:
Die Optimierung der polygonalen Gleitfläche sucht nach der kritischsten Fläche (niedrigster Stabilitätsgrad SF).