Polygonale Gleitläche
Das Programm berechnet die Stabilität der Gesteinsblöcke, die sich über die polygonale Gleitfläche verschieben. Da die allgemeine Lösung sehr komplex ist, verwendet das Berechnungsprogramm die folgenden Annahmen:
- Bewegung von Felsblöcken ist nur translatorisch
- Blöcke verschieben sich entlang der polygonalen Gleitfläche, die entweder durch ebenen Gleitflächen oder durch der mäßig wellenförmigen Gleitflächen gebildet wird
- Felsblöcke sind durch der Fugen mit bekannten Richtungen unterteilt
- tatsächliche Verformung der Gesteinsmasse innerhalb der Blöcke ist vernachlässigbar
- auf der polygonalen Gleitfläche und an der Fugen zwischen der Blöcken gelten die Bruchbedingungen gemäß Mohr-Coulomb
- auf der gesamte polygonale Gleitfläche wird die gleiche Stabilität angenommen
- alle Felsblöcke sind im Kontakt (die Fuge zwischen Blöcken kann nicht öffnen)
Für die Überprüfung der Stabilität der Gesteinsblöcke auf der polygonalen Gleitfläche sind die wichtigsten Eingangsdaten die Scherfestigkeitseigenschaften von Mohr-Coulomb auf der Gleitfläche und in den Fugen, die die einzelnen Blöcke trennen. Die Berechnung wird außerdem durch das Gewicht des Blocks (abhängig von der Geometrie der Gesteinsblöcke und der Wichte von Gesteinen), der Blockverankerung, der Auflast der Blöcke, der Einfluss von Wasser und seismische Effekte beeinflusst.
Die theoretischen Grundlagen der Berechnung werden hier beschrieben.
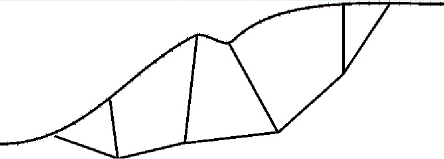 Polygonale Gleitfläche
Polygonale Gleitfläche