Shahunyants
Die Shahunyants-Methode ist ein allgemeines Lamellenverfahren, das auf dem Grenzgleichgewicht beruht. Es benötigt ein befriedingendes Kräftegleichgewicht, das auf einzelne Blöcke wirkt. Die Blöcke (Lamellen) entstehen durch Aufteilen des Bodens über der Gleitfläche durch Trennebenen. Das statische Diagramm und die Kräfte, die auf einen einzelnen Block wirken, sind in der folgenden Abbildung dargestellt:
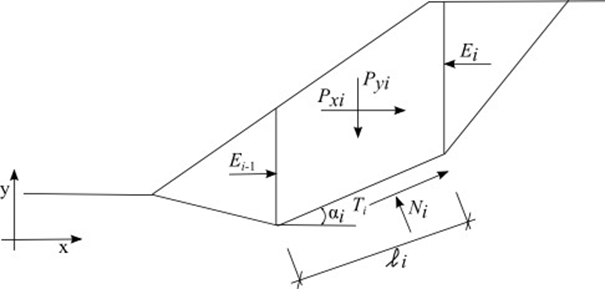 Statisches Schema: Shahunyants-Methode
Statisches Schema: Shahunyants-Methode
Für jeder Block wird die Auswirkung von folgenden Kräfte vorausgesetzt:
wo: | Pyi | - | vertikale Resultierende von Kräften auf einem Block (Blockgewicht, Auflast, Erdbeben, Ankerkraft, …) |
Pxi | - | horizontale Resultierende von Kräften auf einem Block (Auflast, Erdbeben, Ankerkraft, Geobewehrungen, …) | |
Ei+1, Ei | - | Kräfte zwischen den Blöcken | |
Ni | - | Reaktion unter dem Block senkrecht zum Gleitflächenabschnitt | |
Ti | - | Reibungskraft des Gleitflächenabschnitts | |
αi | - | Neigung des Gleitflächenabschnitts | |
li | - | Länge des Gleitflächenabschnitts | |
φi | - | Winkel der inneren Reibung auf dem Gleitflächenabschnitt | |
ci | - | Kohäsion des Bodens auf dem Gleitflächenabschnitt |
Die folgenden Annahmen werden bie der Shahunyants-Methode getroffen, um den Grenzzustand eines Blockes berechnen zu können:
- Trennflächen zwischen den Lamellen sind immer vertikal
- Neigung der Kräfte Ei zwischen den Blöcken ist gleich Null, Kräfte wirken horizontal
Lösungsverfahren:
Die Kräfte Pyi und Pxi werden zuerst mithilfe der Beziehung (1) und (2) in die Richtung der Kräfte Ti und Ni umgewandelt. Für einen positiven Winkel αi (wie in der Darstellung) wirkt die Kraft PNi in entgegengesetzte Richtung zu Ni, die Kraft PQi in entgegengesetzte Richtung zu Ti.
![]() (1)
(1)
![]() (2)
(2)
Die Kräfte entlang des Gleitflächenabschnitts sind gegeben zu:
![]() (3)
(3)
wo: | Ui | - | Porenwasserdruck auf das Gleitflächenabschnitt |
Die Kräftegleichgewichte des Blocks werden erfüllt:
Gleichgewichtsbedingungen senkrecht zum Gleitflächenabschnitt:
![]() (4)
(4)
Gleichgewichtsbedingungen parallel zum Gleitflächenabschnitt:
![]() (5)
(5)
Einsetzen von Gleichung (3) in Gleichung (5) ergibt:
![]() (6)
(6)
Substituiere mit Gleichung (4) in Gleichung (6):
![]() (7)
(7)
Nach Umformungen ergibt sich:
![]() (8)
(8)
Unter Ausnutzung des folgenden mathematischen Ausdrucks:
![]() (9)
(9)
Ergibt sich Gleichung (8) zu:
![]() (10)
(10)
Das kann umgeformt werden zu:
![]() (11)
(11)
Das ergibt den periodischen Ausdruck für die Kräfte Ei zwischen den Blöcken:
![]() (12)
(12)
An diesem Punkt der Berechnung kommt der Sicherheitsfaktor Ku hinzu. Der Sicherheitsfaktor ist der Wert, der auf einzelne Blöcke wirkende Kräfte in den Grenzzustand versetzt. Das wird erreicht, indem man aktive Kräfte, also Kräfte die zum Rutschen der Erdmassen über die Gleitfläche beitragen, mit dem Sicherheitsfaktor multipliziert. Aktive Kräfte sind in Gleichung (12) in der Variable PQi enthalten. Diese Variable enthält sowohl aktive Kräfte, die zum Rutschen beitragen, als auch Kräfte, die einen Widerstand gegen Rutschen darstellen. Die beitragenden Kräfte werden als PQi,sd, die Widerstand leistenden als PQi,ud notiert. Gleichung (12) sieht dann folgendermaßen aus:
![]() (13)
(13)
Wenn der Wert von PQi positiv ist, führt dies zu Rutschen und ist somit die aktive Kraft PQi,sd. Ist PQi negativ, dann liegt Widerstand gegen Rutschen PQi,ud vor. Demnach führt die Subtraktion des negativen Werts PQi,ud letztendlich zu dessen Addition, sodass mach Gleichung (13) folgendermaßen schreiben kann:
![]() (14)
(14)
Am Ursprung der Gleitfläche ist E0 = 0. Der Wert von E1 ist gegeben zu:
![]() (15)
(15)
Demnach ist E2 dann:
![]() (16)
(16)
Auf ähnlichem Weg kann man die Werte aller Kräfte zwischen den Lamellen bestimmen. Am Ende der Gleitfläche gilt En= 0. Unter Verwendung der vorherigen Ausdrücke kann man schreiben:
![]() (17)
(17)
Diese Gleichung liefert direkt den Sicherheitsfaktor Ku in der Form:
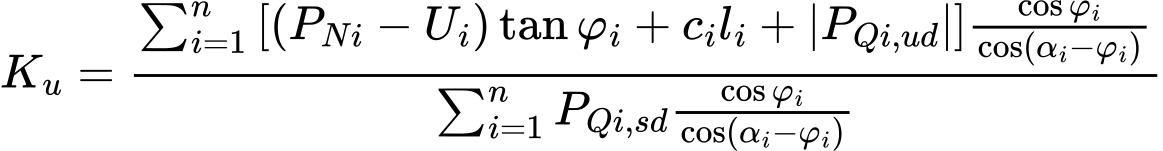 (18)
(18)