Véas-Souche-Methode
Die Ausgangsbeziehung des Verfahrens ist die Gleichung, die die Größe der kritischen Kraft Ncr in Abhängigkeit von der Länge des Mikropfahls lp angibt (siehe Literatur [1]):
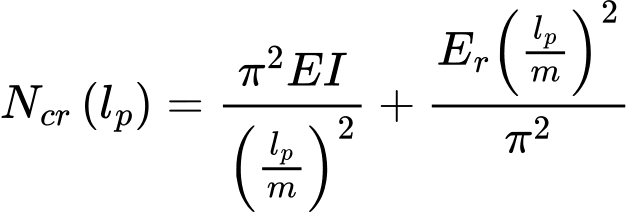
wo: | lp | - | effektive Mikropfahllänge (freie Mikropfahllänge + 1/2 der Wurzellänge) |
EI | - | Biegesteifigkeit der Mikropfahlbewehrung | |
Er | - | ||
m | - | Anzahl der Halbwellen der Biegelinie entlang der Länge des Mikropfahls |
Als Minimum der Funktion (1) wird die kritische Kraft Ncr gesucht. Dies wird für die Länge der Halbwelle erreicht
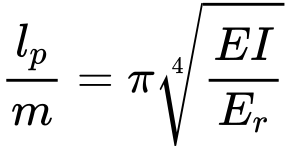
Gleichung (2) gibt die Beziehung für die Anzahl der Halbwellen an m:
![]()
Weiterhin wird eine dimensionslose Größe ω eingeführt, die durch das Verhältnis
![]()
wo: | lv | - | Länge des Mikropfahls über dem Gelände |
und eine weitere dimensionslose Größe, gegeben durch den Ausdruck
![]()
Die Beziehungen zwischen den Größen (3), (4) und (5) werden mit Hilfe von Diagrammen beschrieben, die im Artikel [2] veröffentlicht wurden. Aus diesen Diagrammen werden die Werte der Größe (5) für die angegebenen Werte der Größen ω und m bestimmt und der Wert der kritischen Kraft Ncr berechnet.
Literatur:
[1] Timoshenko, S. P.: Theory of Elastic Stability, New York, 1936
[2] Véase, Souche: Étude du fla,berment de pieux partiellernent immergés dans offrant latéralement une réaction élastique pure, Annales de I’ITBTP, No. 423, Sene Soils et Foundations, 187, mars - avril 1984, str. 38 - 60 (Französisch)