Generalized Cam-Clay Model (GCC)
The Generalized Cam-clay model grounds on the same principles as the Modified Cam-clay model. However, it offers a considerable improvement, namely when modeling the soil in a supercritical domain. Therein, it considerably reduces the degree of softening as well as the predicted shear strength (see the dotted line in the following figure corresponding to the projection of the Modified Cam-clay model into the meridian plane) in the case of highly overconsolidated soils. As evident from the projection of the yield surface into the meridian plane the model follows in the supercritical region (overconsolidation region) the models of the Mohr-Coulomb type. Unlike these models, however, it allows for the modeling of critical state of soils. The projection of the yield surface into the deviatoric plane is described by the Matsuoka-Nakai yield surface which is in accord with all Elasto-plastic models with hardening/softening.
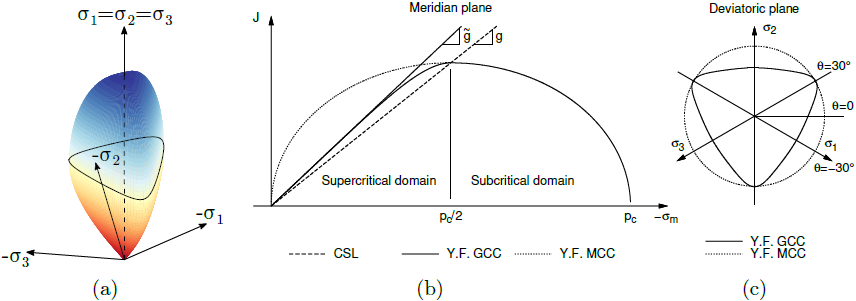 a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
The evolution of preconsoidtion pressure ![]() as well as the meaning of parameters defining the constitutive relations are described in detail in the presentation of the Modified Cam-clay model. Further details are available in the theoretical manual. Parameters defining the Generalized Cam-clay material model are summarized in the following table.
as well as the meaning of parameters defining the constitutive relations are described in detail in the presentation of the Modified Cam-clay model. Further details are available in the theoretical manual. Parameters defining the Generalized Cam-clay material model are summarized in the following table.
Symbol | Units | Description | |
| [-] | Slope of swelling line | |
| [-] | Slope of normal consolidated line | |
| [-] | Maximum void ratio on | |
| [-] | Poisson's ratio | |
| [°] | Critical state friction angle | |
| [°] | Peak angle of internal friction | |
| [kN/m3] | Bulk weight | |
| [-] | Overconsolidation ratio | |
| [kPa] | Preoverburden pressure | |
| [1/°] | Coefficient of thermal expansion (when considering temperature effects) | |
| [kPa] | Preconsolidation pressure |
Contrary to the Modified Cam-clay model the critical state friction angle φcs is one of the input parameters. Apart from that the model introduces the peak angle of internal friction defining the slope ![]() , see the previous figure. Together with the slope of critical state line g (unlike the slope of critical state line Mcs in the Modified Cam-clay model this quantity is not constant owing to the application of Matsuoka-Nakai failure criterion) it is provided by the following expressions:
, see the previous figure. Together with the slope of critical state line g (unlike the slope of critical state line Mcs in the Modified Cam-clay model this quantity is not constant owing to the application of Matsuoka-Nakai failure criterion) it is provided by the following expressions:
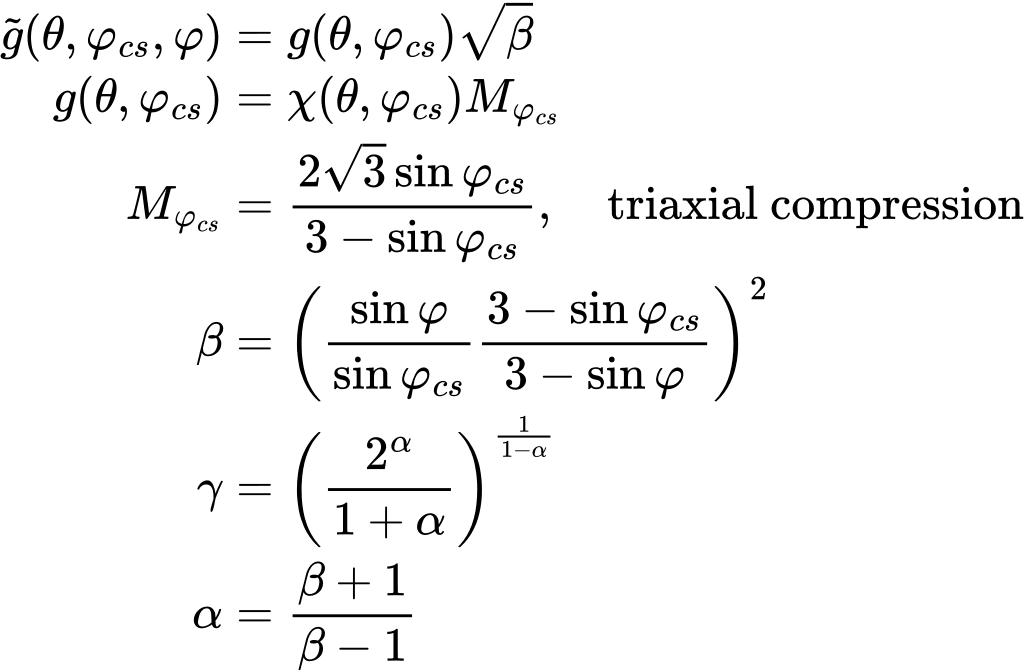
where θ is the Lode angle and function Χ(θ, φcs) defines the shape of the Matsuoka-Nakai failure criterion. Further details can be found in the theoretical manual.
Similarly to the Modified Cam-clay model the modulus of elasticity E is not one of the input parameters, but instead it is determined from the bulk modulus Ks and Poisson's ratio. The bulk modulus is provided by
![]()
The evolution of stiffness, similarly to the Modified Cam-clay model, depends on the mean effective stress σm. This is closely related to the selection of the initial load step, which requires for very low values of initial stress to be sufficiently small. To speed up convergence it appears useful to exploit the Minimum number of iterations for a single load step. The influence of magnitude of the initial load step on the evolution of stress and strain is described in detail here.
Setting up the initial preconsolidation pressure pcin, the initial bulk modulus Kin, and the initial void ratio ein is described in detail in the presentation of the Modified Cam-clay model. The initial void ratio ein, which corresponds to the state at the end of the first calculation stage, is not directly inputted but rather computationally determined from the inputted value of void ratio e0 and the current state of stress.
The model allows for adjusting the initial value of preconsolidation pressure pc in dependence on the expect degree of preconsolidation by using parameters OCR and POP. Details can be found here. Point out that this option is available only when setting the initial geostatic stress with the help of K0 procedure.
Providing the undrained conditions are required in the analysis one may proceed with the Type (1): analysis in effective stress (cef, φe) only.
The Generalized Cam-clay model also allows for performing the stability analysis. However, this option is available only when running the stability analysis analysis within a given construction stage. The task is solved by gradually reducing both the peak angle of internal friction φ and the critical state friction angle φcs as follows
![]()
where ζ is the reduction coefficient, φ, φcs are the actual values of friction angles and φd, φcs, d stand for the reduced parameters. The Factor of safety FS is then given by
![]()
The bulk modulus is kept fixed during the reduction process. It is set equal to the one at the and of the corresponding stress analysis in a given calculation stage.
The model performance in the framework of simple laboratory tests is examined here including a comparative study with the Modified Cam-clay model.
Implementation of the Generalized Cam-clay material model into the GEO5 FEM program is described in detail in the theoretical manual.