Online Súgó

Sarma

El método Sarma corresponde a una categoría de métodos generales de estados límites. Basada en completar las fuerzas y las condiciones de momento de equilibrio en bloques individuales. Los bloques son creados dividiendo el suelo en regiones sobre la superficie de deslizamiento potencial, la cual puede en general, experimentar diferentes inclinaciones. Las fuerzas actuando en bloques individuales se muestran en la figura.

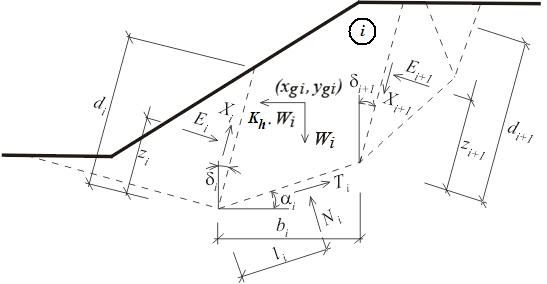Esquema estático – Método Sarma

Aquí:E_i, X_i representa la fuerza normal y de corte entre bloques. N_i, T_i representa la fuerza normal y de corte en segmentos de superficies de deslizamiento. W_i es el peso del corte k_i*W_i es la fuerza horizontal que se utiliza en el método Sarma para alcanzar el estado límite. Generalmente sobrecargas inclinadas pueden ser introducidas en cada bloque. Estas sobrecargas se incluyen en el análisis junto con la sobrecarga debido al agua teniendo el nivel freático por encima del terreno y con fuerzas en anclajes. Todas esas fuerzas son proyectadas a lo largo de las direcciones horizontales y verticales, las cuales luego se resumen en  Fx_i y Fy_i.

K_h es una constante llamada Factor de aceleración horizontal y se ingresa en el análisis con el fin de satisfacer el equilibrio de los bloques individuales. Existe una relación entre K_h y el factor de estabilidad de talud SF que permite el cálculo del  factor de seguridad. En circunstancias normales el análisis continúa con el valor de K_h igual a cero. Un valor de K_h no nulo se utiliza para simular una sobrecarga horizontal, ejemplo: Debido a sismo (vea debajo).

Proceso de análisis

Cálculo de límites de equilibrio

El cálculo de los límites de equilibrio requiere de una solución de 6n - 1 incógnitas, donde n números se mantienen para bloques de regiones de suelos sobre la superficie de deslizamiento potencial. Estas son:

5n-1 ecuaciones están disponibles para las incógnitas requeridas. En particular, se tiene:

a) Ecuaciones de fuerzas horizontales de equilibrio en bloques:

b) Ecuaciones de fuerzas verticales de equilibrio en bloques:

c) Ecuaciones de momento de equilibrio en bloques:

Donde rx_i y ry_i son los brazos de las fuerzas Fx_i y Fy_i.

d) Relación entre la fuerza normal y la fuerza de corte de acuerdo a la teoría de Mohr-Coulomb:

Es evidente que: n-1 debe ser seleccionada como prioridad. Pequeños errores relativos se reciben cuando estimamos puntos de aplicación de fuerzas E_i. El problema entonces de vuelve estáticamente determinado. Resolviendo el sistema de ecuaciones resultante, finalmente se provee el valor de las restantes incógnitas. El principal resultado de este análisis es la determinación del factor de aceleración horizontal k.

Cálculo de factor de estabilidad de talud SF

El factor de estabilidad de talud SF se introduce en el análisis como para reducir los parámetros de resistencia del suelo c y tgφ. El análisis de equilibrio se realiza luego por parámetros reducidos a llegar al factor de aceleración horizontal pertinente K_h a un determinado factor de estabilidad de talud SF. Esta iteración se repite hasta que el factor K_h llega a cero o a algún valor específico.

Influencia de cargas externas

El talud analizado puede ser cargado en su tierra por una carga inclinada que tiene una forma general trapezoidal. Estas caras introducen en el análisis material componentes verticales (si se tiene la dirección del peso) se agrega al peso correspondiente al bloque. Este resultado cambia ambos, el peso del corte y el centro de gravedad. Proporcionando la componente vertical que actúa contra la dirección de la gravedad se agrega a la fuerza Fy_i. La componente horizontal se agrega a la fuerza Fx_i.

Bibliografía:

Sarma, S. K.: Stability analysis of embankments and slopes,Géotechnique 23, 423–433, 1973.