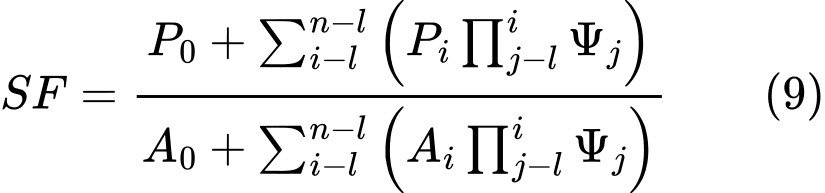Méthode ITF (Imbalance Thrust Force)
La méthode ITF est une méthode d'état limite. Elle repose sur l'équation d'équilibre des forces agissant sur des blocs individuels et ne prend pas en compte l'équation d'équilibre des moments. Les bases de la méthode et les hypothèses adoptées sont claires à partir de la figure suivante.
 Méthode ITF - Forces agissant sur un bloc
Méthode ITF - Forces agissant sur un bloc
On considère les hypothèses suivantes concernant les forces agissant sur le bloc :
où : | Wi | - | poids du ième bloc, le poids d'une partie de bloc sous le niveau d'eau est calculé à partir du poids volumique du sol saturé γsat |
Fyi | - | autres charges verticales agissant sur le bloc | |
Fxi | - | autres charges horizontales agissant sur le bloc | |
Fi, Fi+1 | - | forces agissant entres les blocs le long des directions données par les angles αi et αi+1 |
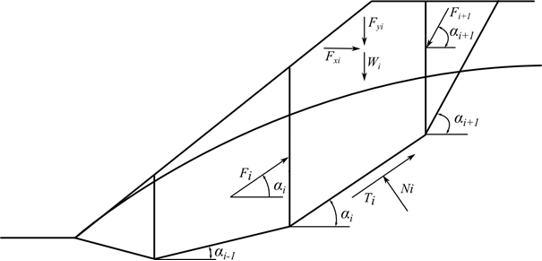
 Schéma de l'action de la pression interstitielle sur un bloc
Schéma de l'action de la pression interstitielle sur un bloc
Ui | - | résultante de la pression interstitielle sur un segment de surface de glissement | |
UVi,UVi+1 | - | résultante de la pression interstitielle sur les plans de division entre les blocs |
Les forces UVi et UVi+1 sont incluses dans les forces horizontales Fxi.
L'équation d'équilibre des forces dans la direction perpendiculaire au segment de la surface de glissement fournit :
![]()
Les forces sur le segment d'une surface de glissement sont liées par :
![]()
où : | φi | - | angle de frottement interne du sol |
ci | - | cohésion du sol | |
li | - | Longueur du segment de surface de glissement lié au ième bloc |
L'équation d'équilibre des forces dans la direction du ième segment de la surface de glissement (donnée par l'angle αi) donne la force Fi agissant entre les blocs sous la forme :
![]()
En introduisant l'équation (1) dans l'équation (2), puis en substituant la valeur de Ni ainsi obtenu dans (3), on obtient :
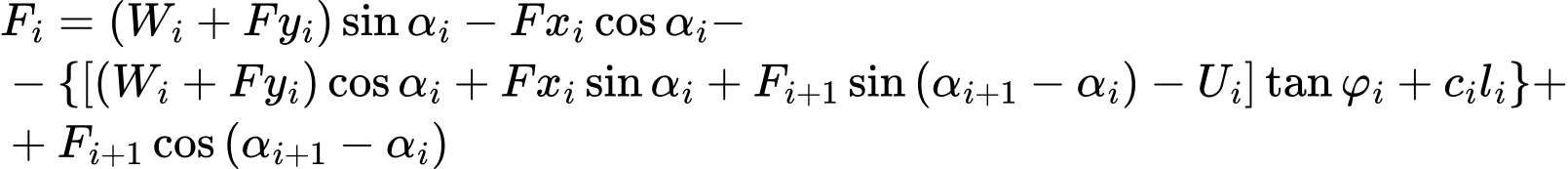
quelques manipulations algébriques permettent d'arriver à la forme suivante :
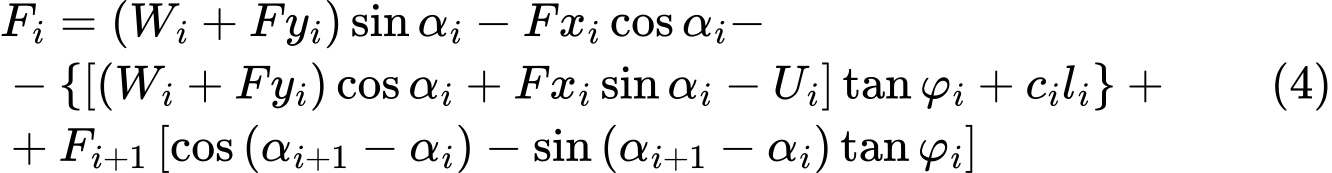
La condition d'équilibre est satisfaite en introduisant le coefficient de sécurité SF dans le calcul de sorte que les paramètres de résistance du sol c et tanφ soient divisés par cette valeur. L'équation (4) devient alors :
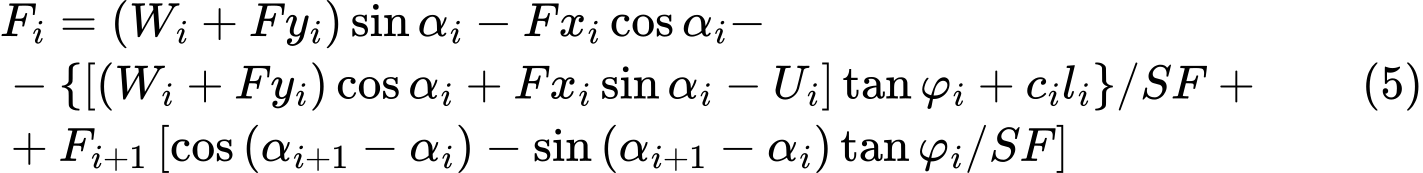
L'équation (5) donne alors le coefficient de sécurité recherché SF par le processus itératif. Ce processus se déroule de sorte que la force Fn soit nulle au point le plus haut (extrémité) de la surface de glissement. Les forces Fi agissant entre les blocs sont déterminées pour une valeur donnée du coefficient de sécurité SF de l'équation (5). Cette étape est répétée pour différentes valeurs de SF jusqu'à ce que l'on trouve un SF pour lequel la force F0 à la base de la pente devienne nulle. Aucune tension n'est supposée le long de la surface de glissement. Si la condition d'équilibre nécessite que la valeur de la force normale Ni soit négative, ce qui signifie que le sol est chargé en tension, la valeur de cette force est égale à zéro lors de la prochaine itération et la force de cisaillement Ti agissant sur un segment donné est déterminé uniquement en fonction de la cohésion du sol.
La méthode ITF est assez sensible à la géométrie de la surface de glissement. Dans le cas où la surface de glissement présente des discontinuités de segment brusques, le coefficient de sécurité résultant est généralement plus grand qu'en réalité. Il est recommandé que la différence de pente entre les segments adjacents de la surface de glissement soit inférieure à 10°. Le programme vérifie automatiquement cette hypothèse et si la différence de pente est plus grande, le programme vous avertit que les résultats peuvent être surestimés. Ce n'est généralement pas le cas pour une surface de glissement circulaire, mais il faut en tenir compte en cas de surfaces de glissement polygonales.
Méthode ITF - solution explicite
La méthode ITF propose d'introduire le coefficient de sécurité explicitement (la solution mathématique ne requiert pas de relation de récurrence) : le coefficient de sécurité est calculé directement en une étape. En utilisant cette approche, la valeur du coefficient de sécurité résultant est généralement plus grande que de raison, ce qui peut totalement déprécier la qualité de la solution (particulièrement lorsque les surfaces de glissement polygonales présentent de larges écarts de pente entre deux segments adjacents).
La solution utilise l'équation (4), dans laquelle le coefficient de sécurité SF est introduit comme multiplicateur des composantes actives des forces (c'est-à-dire les composante agissant dans la direction du glissement). La condition d'équilibre devient alors :
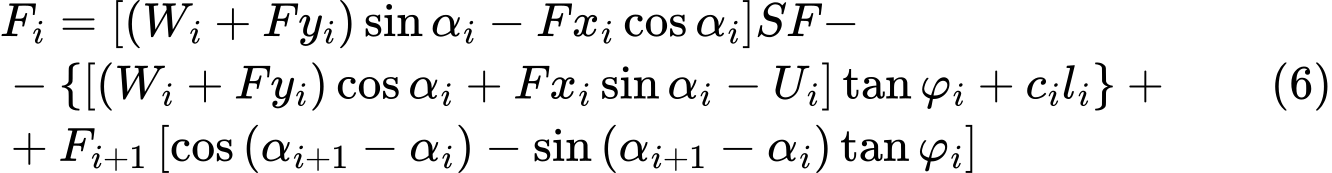
Pour des raisons de clarté, la composante des forces actives est définie par :
![]()
la composante des forces passives par :
![]()
enfin on introduit la fonction auxiliaire :
![]()
L'équation (6) prend alors la forme plus compacte suivante :
![]()
En partant de la valeur de force connue Fn = 0, on construit les expressions pour les forces inter-blocs F :
![]()
![]()
![]()
De là, on obtient :
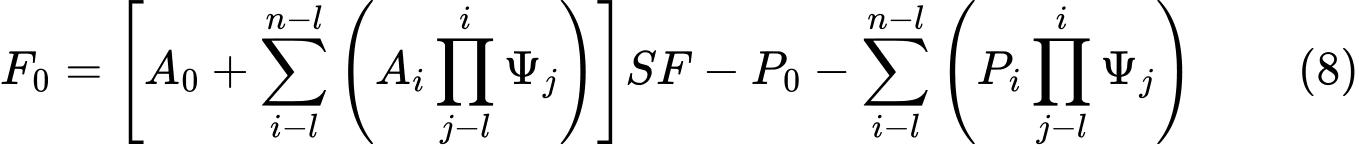
Et comme la force F0 à l'extrémité inférieure de la surface de glissement doit être égale à 0 kN, le coefficient de sécurité SF peut être exprimé par: