Online Súgó

Sarma

O método de Sarma consiste num método geral de divisões dos estados limite. Este método baseia-se em completar as condições de equilíbrio dos momentos e forças que atuam em cada bloco. Os blocos são criados a partir da divisão da região do solo acima da potencial superfície de deslizamento, através de planos, que podem ter inclinações diferentes. A figura mostra as forças que atuam em cada bloco.

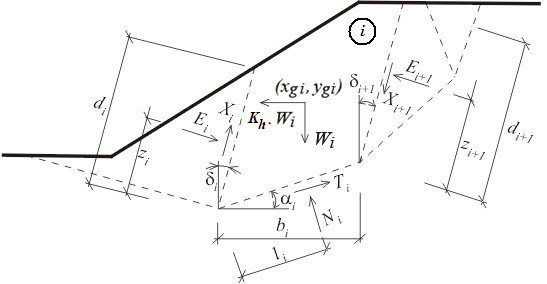Esquema das forças atuantes - Método de Sarma

Aqui, E_i , X_i representam as forças normal e de cisalhamento entre blocos. N_i , T_i  representam as forças normal e de cisalhamento nos segmentos da superfície de deslizamento. W_i representa o peso do bloco e K_h*W_i  representa a força horizontal utilizada para atingir o estado limite no método de Sarma. Podem ser introduzidas sobrecargas inclinadas a cada bloco. Esta sobrecarga é incluída na análise juntamente com a sobrecarga devido ao nível freático, quando este se encontra acima do bloco em análise, e as forças das ancoragens. Estas forças são projetadas nas direções horizontal e vertical, sendo resumidas nas componentes Fx_i e Fy_i.

K_h é a constante que define o fator de aceleração horizontal e é introduzida na análise para satisfazer o equilíbrio de cada bloco. Existe uma relação entre o K_h e o fator de estabilidade do talude que permite que a computação do fator de segurança FS. Em situações normais, a análise é executada com o valor de K_h igual a zero. Um valor diferente de zero para K_h é utilizado para simular a sobrecarga horizontal, ex.: devido a um sismo (ver em baixo).

Processo da análise

Computação do equilíbrio limite

A computação do equilíbrio limite requer a resolução de 6n - 1 incógnitas, onde n representa o número de blocos que divide a região do solo acima da superfície de deslizamento potencial. Estas são:

5n - 1 equações estão disponíveis para determinar as incógnitas. Em particular, temos:

a) equação de equilíbrio do bloco para as forças horizontais:

b) equação de equilíbrio do bloco para as forças verticais:

c) equação de equilíbrio do bloco para momentos:

onde rx_i e ry_i representam o braço das forças Fx_i e Fy_i

d) relação entre as forças normal e de cisalhamento de acordo com a teoria de Mohr-Coulomb:

É evidente que n - 1 devem ser selecionadas (estimadas) com prioridade. Existe um erro relativamente pequeno na estimativa dos pontos de aplicação das forças E_i. O problema passa a ser estaticamente determinado. Ao resolver o sistema de equações é possível determinar os valores de todas as incógnitas. O resultado principal desta análise é a determinação do fator de aceleração horizontal K_h.

Computação do fator de segurança da estabilidade do talude FS

O fator de segurança da estabilidade do talude FS é introduzido na análise de forma a reduzir os parâmetros c e tgφ do solo. A análise de equilíbrio é realizada de acordo com os parâmetros reduzidos do solo para obter um valor do fator horizontal de aceleração K_h que permita verificar a estabilidade do talude de acordo com o fator de segurança SF pretendido. Este cálculo é um processo iterativo que se repete até que o fator K_h seja igual a zero ou a um valor desejado.

Influência de cargas externas

O talude em análise pode ser carregado por forças trapezoidais inclinadas. Para a análise de estabilidade, estas cargas são consideradas de maneira a que a componente material vertical (caso possua a mesma direção que o peso) seja adicionada ao peso do bloco em estudo. Isto irá alterar o peso do bloco e a posição do seu centro de gravidade. Se a direção da componente vertical for inversa à da gravidade, o valor da componente vertical será adicionado à força Fy_i. A componente horizontal é adicionada à força Fx_i.

Bibliografia:

Sarma, S. K.: Stability analysis of embankments and slopes, Géotechnique 23, 423-433, 1973.