Online Súgó

Shahunyants

El método Shahunyants es un método general de capas desarrollado sobre la base de equilibrio límite. Se requiere un equilibrio satisfactorio de las fuerzas y momentos que actúan sobre bloques individuales. Los bloques se crean mediante la división del suelo por encima de la superficie de deslizamiento por los planos de división. Las fuerzas que actúan sobre bloques individuales se muestran en la siguiente figura:

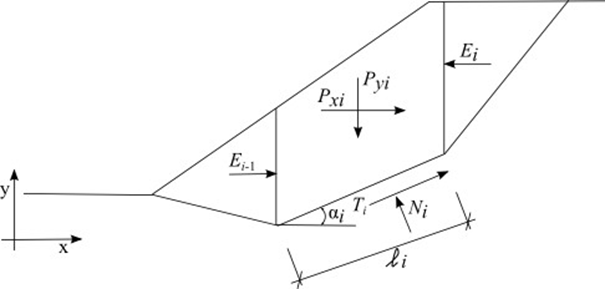Esquema estático - Método Shahunyants

Cada bloque asume la acción de las siguientes fuerzas:

Las siguientes suposiciones adoptan el método Shahunyants para calcular el estado límite en un determinado bloque:

• los planos divisorios entre los bloques son siempre verticales
• pendiente de fuerzas E_i que actúa entre los bloques es igual a cero, las fuerzas actúan horizontalmente

Procedimiento de solución:

Las uerzas P_yi y P_xi se transforman primero con la ayuda de las expresiones (1) y (2) en las direcciones de las fuerzas T_i y N_i. Para un ángulo α_i positivo (de la misma forma que en el esquema) la fuerza P_Ni actúa en la dirección opuesta a N_i, la fuerza P_Qi actúa en la dirección opuesta a T_i.

(1)

(2)

Las fuerzas que actúan a lo largo del segmento de superficie de deslizamiento están relacionadas por:

(3)

La fuerza de las ecuaciones de equilibrio se cumplen en el bloque:

La condición de equilibrio en la dirección normal al segmento de superficie de deslizamiento:

(4)

La condición de equilibrio en la dirección paralela al segmento de superficie de deslizamiento:

(5)

Ingresando la ecuación. (3) en la ecuación. (5) se obtiene:

(6)

A continuación, sustituyendo la ecuación. (4) en la ecuación. (6) se obtiene:

(7)

luego de algo de algebra:

(8)

Explotando la siguiente expresión matemática:

(9)

Eq. (8) en la forma:

(10)

Esto puede ser modificado como:

(11)

para proporcionar la expresión recurrente para las fuerzas E_i que actúan entre bloques como:

(12)

En esta etapa el análisis ingresa en el factor de seguridad K_u. El factor de seguridad es el valor que aportan las fuerzas que actúan sobre bloques individuales de suelo en el estado de los estados límites. Esto se logra multiplicando fuerzas activas, es decir, las fuerzas que contribuyen al deslizamiento de la masa de suelo por encima de la superficie de deslizamiento, por el factor de seguridad. Las fuerzas activas están contenidas en la ecuación (12) por el término P_Qi. Este término contiene por un lado las fuerzas activas que contribuyen al deslizamiento y por otro lado las otras fuerzas que se resisten al deslizamiento. Las fuerzas que contribuyen se indican como P_{Qi, sd}, mientras que las fuerzas de resistencia como P_{Qi, ud}. La Ecuación (12) se convierte en:

(13)

Proporcionando el valor de P_Qi como positivo, entonces se contribuye al deslizamiento y se asume como fuerza activa P_{Qi, sd}. Proporcionando el valor de P_Qi como negativo, se resiste al deslizamieto y se asume como fuerza P_{Qi, ud}. Por lo tanto restando el valor P_{Qi, UD}, que es negativo, en la ecuación (13) significa que se agrega esencialmente el valor positivo, por lo que podemos escribir formalmente:

(14)

En el origen de la superficie de deslizamiento el valor de E₀ = 0 El valor de E₁ viene dado por:

(15)

El valor de E₂ está dado por:

(16)

Del mismo modo es posible determinar los valores de todas las fuerzas que actúan entre bloques. Se considera además en el punto final de la superficie de deslizamiento que tenemos E_n = 0. Aprovechando las expresiones anteriores, esto puede escribirse como:

(17)

Esta ecuación proporciona directamente el factor de seguridad K_u en la forma:

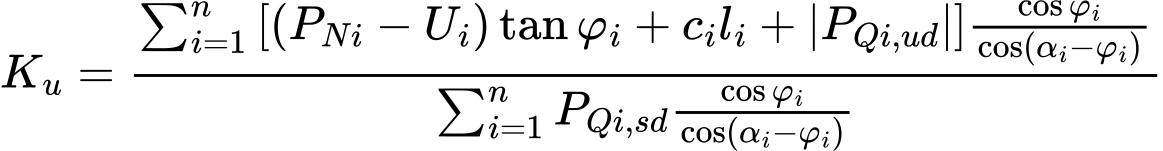(18)